г) метод найменших квадратів Гауса служить як критерій апроксимації: інтеграл по квадратних різницях повинен мати лінійне значення:
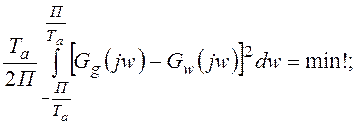
д)
похибка апроксимації мінімальна в середньому квадратичному, якщо вагові
коефіцієнти ![]() шуканого фільтра є
коефіцієнтами Фур’є, розвинуті в ряд
шуканого фільтра є
коефіцієнтами Фур’є, розвинуті в ряд ![]() .
.
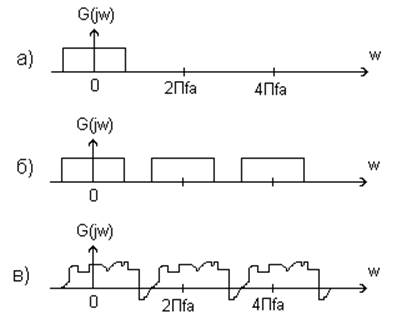
Рис.3
За допомогою наведеного вище алгоритму можна визначити шукані коефіцієнти фільтра. Бажаним є ідеальний ФНЧ з передаточною функцією
![]() при
при ![]()
![]() – парна функція;
– парна функція;
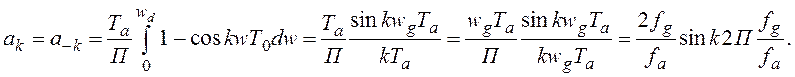 Коефіцієнти
Коефіцієнти
![]() обчислюються із
функції розщеплення, в якій аргументом буде відношення граничної частоти до
частоти вибірок. Ці обидві величини в усіх випадках зв’язані одна з
одною, якщо в уже визначеному фільтрі буде змінена частота
дискретизації, то зміниться також і гранична частота. З цієї причини при
визначенні параметрів фільтрів буде часто обчислюватися гранична циклічна
частота, віднесена до частоти дискретизації:
обчислюються із
функції розщеплення, в якій аргументом буде відношення граничної частоти до
частоти вибірок. Ці обидві величини в усіх випадках зв’язані одна з
одною, якщо в уже визначеному фільтрі буде змінена частота
дискретизації, то зміниться також і гранична частота. З цієї причини при
визначенні параметрів фільтрів буде часто обчислюватися гранична циклічна
частота, віднесена до частоти дискретизації:
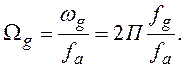
Коефіцієнти ФВЧ шукаються, виходячи вже з відомих коефіцієнтів ФНЧ:
![]()
![]() –
коефіцієнти високочастотного фільтра.
–
коефіцієнти високочастотного фільтра.
Цей процес можна проілюструвати за допомогою рис.4.

Рис.4
За допомогою wavelet перетворення можна в більш компактному вигляді представити широкий спектр сигналів. Зокрема, переривчастої функції та функції з гострими піками звичайно потребують істотно менше базових wavelet-функції ніж sin-cos базових функцій при схожих апроксимованих виглядах. Ця властивість робить wavelet чудовим інструментом для компресії даних. Наприклад, wavelet перетворення знаходять застосування в таких новітніх технологіях, як мультимедіа, при стисненні аудіо сигналів з широкою частотною смугою.
Проблема компресії звукових сигналів виникла в області комунікації мультимедіа при стискуванні аудіосигналів з широкою частотною смугою. В даний час швидкість передачі якісного аудіосигналу не дозволяє їх використовувати в багатьох мультимедіа платформах, таких як персональні комп’ютери. Одним із шляхів подолання цієї перешкоди є компресія даних і сигналів.
Область застосування широкосмугового аудіо досить широка. Вона вимагає мультимедійні документи, CD-ROM, комп’ютерні ігри, відео, віртуальну реальність, голосову електронну пошту тощо. Багато зусиль було прикладено, щоб вирішити проблему зберігання і передачі величезних об’єктів інформації. Саме тут стало в пригоді стиснення за допомогою wavelet перетворення.
Частотна смуга широкосмугового сигналу обмежена діапазоном 20Гц-20кГц. Але енергетичний спектр в цій смузі не однаковий. Цей нерівний розподіл дає нам мотивацію для використання розкладу сигналів. З точки зору теорії сигналів резонно уважніше віднестися до сигналів з високою енергією.
Оскільки wavelet перетворення добре представляє сигнали з гострими піками, то його з успіхом можна використовувати для очистки від шумів.
Слід відмітити, що wavelet перетворення використовується і в інших галузях науки і техніки. Зокрема, передбачається використання методів wavelet аналізу для перетворення енергетичних параметрів (потужність, енергія, діючі значення напруг і струмів).
Wavelet перетворення дуже добре підходить для обробки короткотривалих імпульсних сигналів, а саме такі сигнали найчастіше зустрічаються на практиці.
ДИСКРЕТЕ WAVELET ПЕРЕТВОРЕННЯ
Дискретне wavelet перетворення в своїй основі має ієрархічну структуру. Воно спочатку застосовується до повного вектора даних довжиною N, потім до згладжуючого вектора довжиною N/2, потім до згладженого вектора довжиною N/4 і т.д., аж поки не залишиться незначне число компонент. Таку процедуру називають ″пірамідальним алгоритмом″.
Вихід DWT складається з залишків компонентів і всіх ″детальних″ компонент, що були накопичені під час всього перетворення. На рис.5 приведена структура DWT, яка використовується в даній курсовій роботі і розрахована на 16 вхідних вибірок і відповідно на 3 послідовно включені комірки.
Значення
![]() і-ого рівня (і-та
комірка) названа ″wavelet коефіцієнтом″ початкового вектора даних, а кінцеві
значення
і-ого рівня (і-та
комірка) названа ″wavelet коефіцієнтом″ початкового вектора даних, а кінцеві
значення ![]() повинні називатись
базовими функціональними коефіцієнтами. В курсовій роботі коефіцієнти
повинні називатись
базовими функціональними коефіцієнтами. В курсовій роботі коефіцієнти ![]() названі wavelet коефіцієнтами
названі wavelet коефіцієнтами ![]() Для організації IDWT потрібно провести зворотну процедуру, починаючи з
найменшого рівня ієрархії. При цьому всі дії (рис.5) треба виконувати справа
наліво і схема зворотного DWT перетворення формує сигнали запиту на передачу
коефіцієнтів
Для організації IDWT потрібно провести зворотну процедуру, починаючи з
найменшого рівня ієрархії. При цьому всі дії (рис.5) треба виконувати справа
наліво і схема зворотного DWT перетворення формує сигнали запиту на передачу
коефіцієнтів ![]() або
або ![]() які поступають на
схему прямого DWT.
які поступають на
схему прямого DWT.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.