Зворотне wavelet перетворення

МІНІСТЕРСТВО ОСВІТИ, НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ «ЛЬВІВСЬКА ПОЛІТЕХНІКА»

ІНСТИТУТ КОМП’ЮТЕРНИХ ТЕХНОЛОГІЙ, АВТОМАТИКИ ТА МЕТРОЛОГІЇ

Кафедра КСА

Пояснювальна записка

до курсового проекту

з курсу

«Проектування та програмування

мікропроцесорних пристроїв автоматики»

на тему

«Зворотне wavelet перетворення»

Виконав

 студент групи КСАм-14

.

Прийняв:

Львів – 2011

Зміст

Вступ ---------------------------------------------------------------------------------------------  3 Опис цифрових фільтрів ---------------------------------------------------------------------- 7 Дискретне wavelet перетворення ---------------------------------------------------------- 10 Опис принципової схеми -------------------------------------------------------------------- 12 Блок-схема алгоритму зворотного перетворення -------------------------------------- 13 Розподіл пам’яті ------------------------------------------------------------------------------- 16 Текст програми -------------------------------------------------------------------------------- 17 Застосування wavelet перетворення ------------------------------------------------------- 20 Література -------------------------------------------------------------------------------------- 21

ВСТУП

Теорія «малохвильового аналізу даних» з’явилася внаслідок досягнень вищої математики у галузі обробки сигналів. Інакше називають «wavelet аналізом».

Слово «wavelet» в перекладі з англійської мови означає елементарну хвилю wavelet – це функція, яка задовольняє певні умови, наприклад, рівність нулю її інтеграла при проходженні вище і нижче осі х. Така симетрія дає функцію, яка може добре локалізуватися.

Подібна синусу та косинусу в Фур’є аналізі, Wavelet використовується як базисна функція для представлення інших функцій. Але є суттєва різниця між Фур’є аналізом і Wavelet. Базові функції Фур’є локалізовані в частотній області, але не в часовій.

Незначні частотні зміни в Фур’є перетворенні спричинятимуть до змін в часовій області. Завдяки цьому багато класів функцій може бути представлена за допомогою wavelet в більш компактному вигляді.

Наприклад, переривчасті функції та функції з гострими піками потребують істотно менше базових wavelet функцій, ніж sin-cos базових функцій. Взагалі перетворення Фур’є можна вважати частковим випадком більш загальної теорії «мальхвильового аналізу сигналів». Один з алгоритмів дискретного wavelet перетворення (DWT) базується на основі швидкого перетворення Фур’є (FFT). Але отримується wavelet перетворення ще швидше, ніж перетворення Фур’є. Відомо, що складність обчислення FFT складає 0 (n log(n)). Для швидкого wavelet перетворення складність знижується до 0(n).

Wavelet перетворення стало добре відомим як корисний інструмент для різних сигнальних перетворень. Напівдискретне wavelet перетворення (wavelet послідовності або ряди) і повністю дискретне можна використовувати для кодування сигналів, зокрема стискування зображень та різні задачі комп’ютерної обробки видимих об’єктів.

Нехай нам даний змінний в часі сигнал . Іноді wavelet перетворення буде складатися з обчислення коефіцієнтів, які є добутками сигналу сімейства «Wavelet». В неперервному перетворенні wavelet, який відповідає масштабу і розміщенню в часі і записується так:

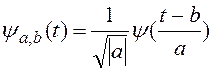,                                                                                       (1)

де – це wavelet-прототип, який може бути смуговою (смугово-пропускною функцією).

Множник  використаний для забезпечення збереження енергії.

Дискретне wavelet перетворення (DWT) було призначене природним wavelet перетворенням для дискретних в часі сигналів. І час, і часо-масштабні параметри у ньому є дискретними.

Фільтровий набір має регулярну обчислювальну структуру, яка реалізується повторним використанням ідентичних комірок. Крім того, така структура має вищу обчислювальну ефективність. Отже, якщо wavelet перетворення вдасться звести до DWT, то його реалізація швидше всього буде ефективною.

В даній роботі використовується стандартний DWT, коефіцієнти якого вибрані на бінарній решітці:   в часо-масштабній площині.

DWT використовується для дискретних в часі сигналів x[n], n є Z. Воно здійснює багаторазовий розклад x[n] на j октавах.

Розклад здійснюється з різною роздільною здатністю наступним чином:

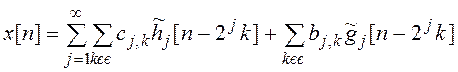                                              (2)

 – дискретний еквівалент

Для забезпечення якісного відновлення використовується додатковий (низькопропускний) елемент:;відповідна базова функція  називається «масштабною послідовністю».

DWT обчислює wavelet коефіцієнти  для  і масштабні коефіцієнти  наступним чином:

                                              (3)

                                                                                    (4)

Розглянемо реакції двох фільтрів h[n] i g[n] (h стоїть для високого пропускання, а g – для низького пропускання). Wavelet і масштабні послідовності отримані ітеративно:

                                                                               (5)

Серед всіх типів wavelet перетворень DWT є одним з тих, які можна обчислити точно. Ми використовуємо дискретний в часі підхід для обрахунку коефіцієнтів wavelet.

Аналоговий вхідний сигнал x(t) дискретизують від самого початку і протягом всього часу, поки триває обчислення в дискретному часі.

Очевидним шляхом дискретизації вхідного сигналу є його вибірка:

                                                                                                      (6)