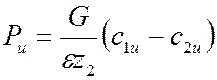Проект паровой турбины: Методические указания к курсовому проектированию по дисциплине "Энергетические машины", страница 19

,                                           (8.10)

Рис. 8.3. Треугольники скоростей турбинной ступени

где  - массовый расход пара через ступень, кг/сек; - степень парциальности; - число рабочих лопаток; - проекция абсолютной скорости выхода пара из сопел на направление окружной скорости, м/сек;    - проекция абсолютной скорости выхода пара из рабочих лопаток на направление окружной скорости, м/сек.

Следует обратить особое внимание на то, что на рис. 8.3 при угле  скорость С_2u является отрицательной, и в этом случае в формуле (8.10) знак минус меняется на плюс.

Осевая составляющая парового усилия обуславливается как динамическим действием рабочей среды при обтекании лопатки, так и разностью статических давлений по обе стороны лопатки:

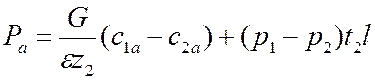      ,                                    (8.11)

где и - осевые составляющие скоростей (см. рис. 8.3), м/сек;                         и -  давление перед и за рабочей решеткой, Па;  - шаг лопаток, м;            - высота лопатки, м.

При подсчете сил по приведенным выше формулам необходимо выбирать режим работы турбины, при котором окружное усилие достигает максимальной величины. Для большинства ступеней турбины, и в особенности для последней ступени, таким режимом является максимальная нагрузка турбины; для первой ступени паровой турбины с сопловым парораспределением опасным режимом служит нагрузка, соответствующая полному открытию первого регулирующего клапана (остальные клапаны закрыты), когда ступень работает с большим тепловым перепадом и малой парциальностью.

Рис. 8.4.  Силы, изгибающие лопатку

 

Равнодействующая сил Р_u  и  Р_а (рис. 8.4) равна их геометрической сумме:

.                                               (8.12)

Для определения напряжений изгиба необходимо найти положение главных центральных осей инерции сечения  и , проходящих через центр тяжести профиля . Силы, действующие в плоскостях наименьшей (ось ) и наибольшей (ось ) жесткости профиля, обозначенные соответственно и , находятся следующим образом:

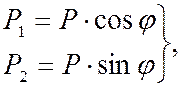                                                  (8.13)

где угол между направлением силы  и перпендикуляром оси минимального момента инерции.

Относительно короткую лопатку (при ) обычно рассматривают как консольную балку с жестко заделанным концом и равномерно распределенной по длине нагрузкой, т.е. пренебрегают переменностью как давлений, так и скоростей по высоте лопатки. В этом случае изгибающие моменты в корневом сечении лопатки равны:

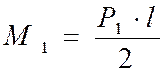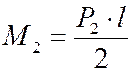,       .                                 (8.14)

Данная методика довольно сложна, поэтому для наших расчетов можно применить следующие упрощения:

1)  ось  минимального момента инерции без большой погрешности может быть принята параллельной хорде профиля  (рис. 8.4);

2)  направление силы  может быть принято совпадающим с осью , так как угол  между ними обычно невелик и

Таким образом, определив по формуле изгибающий момент от газовых сил, можно найти максимальное напряжение изгиба в обеих кромках корневого сечения:

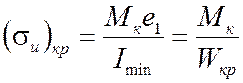                                      (8.15)

и в спинке

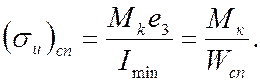                                       (8.15а)

В формулах (8.15) и (8.15а) через  обозначен момент инерции сечения профиля относительно оси , а через W_кр и W_сп –минимальные моменты сопротивления соответственно кромки и спинки сечения лопатки относительно той же оси. Напряжениями в кромках, вызванными моментом от проекции силы Р на ось , т.е. силой Р₂,  можно пренебречь.

На лопатку, изогнутую силами пара, действует центробежная сила ее массы, которая стремится выпрямить лопатку и поэтому создает момент, обратный моменту сил пара. С учетом этого влияния центробежной силы результирующий изгибающий момент равен не величине М, а , где       - так называемый коэффициент разгрузки, меньший единицы. В данной работе расчет коэффициента разгрузки отсутствует.