Исследование устойчивости и качества систем

Практическая работа №6.

Исследование устойчивости и качества систем.

Задание:

Пусть система автоматического регулирования описывается дифференциальным уравнением вида:

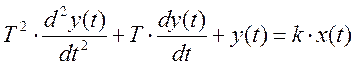
где k=33

       Т=0,№ по списку

Провести анализ устойчивости и оценку качества.

1.  Проведем анализ устойчивости.

Система называется устойчивой, если при подаче на ее вход некоторого возмущающего воздействия через некоторый промежуток времени она возвращается в устойчивое состояние.

При определении устойчивости по дифференциальному уравнению сначала определяют корни характеристического уравнения; если все корни располагаются в левой полуплоскости комплексной плоскости, то система устойчива, если хотя бы один корень располагается на мнимой оси, то система находится на гране устойчивости, если же в правой полуплоскости – система будет неустойчивой.

1.1. Перейдем к преобразованному по Лапласу виду дифференциального уравнения.

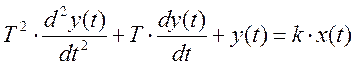
1.2. Упростим выражение (1).

Выражение, стоящее в скобках является характеристическим многочленом. Приравняв его к 0, получим характеристическое уравнение.

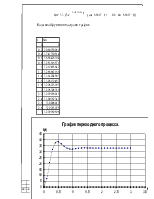
1.3. Найдем корни характеристического уравнения.

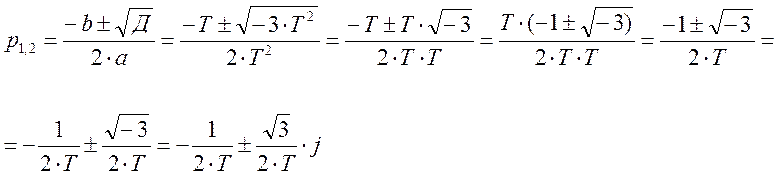
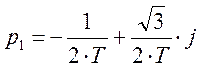
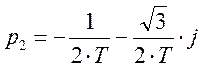
при Т равном 0,№ по списку получим.

Из графика видно, что оба корня находятся в левой полуплоскости комплексной плоскости, значит система будет устойчивой.

2. Оценка качества системы.

Оценку качества можно проводить по прямым или косвенным методам.

Прямые методы оценки качества проводятся по графику переходного процесса, то есть по h(t).

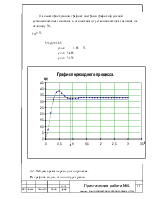
2.1. Построим для заданного уравнения график переходного процесса.

Определим передаточную функцию.

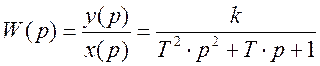
Используя связь между передаточной и переходной функцией, определим переходную функцию.

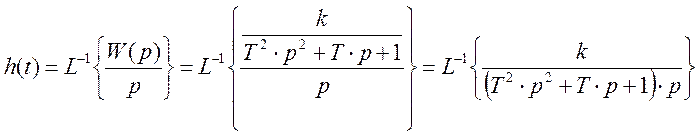
Для нахождения оригинала от изображения, разложим дробь 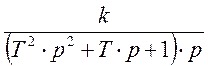 на простые дроби по методу неопределенных коэффициентов.

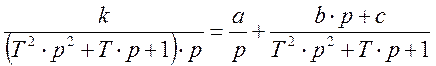
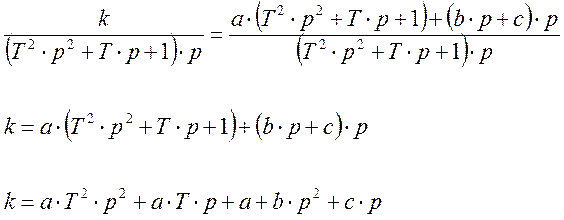
Приравняем коэффициенты и решим получившуюся систему уравнений.

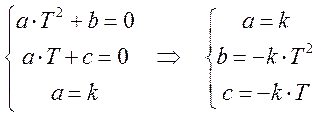
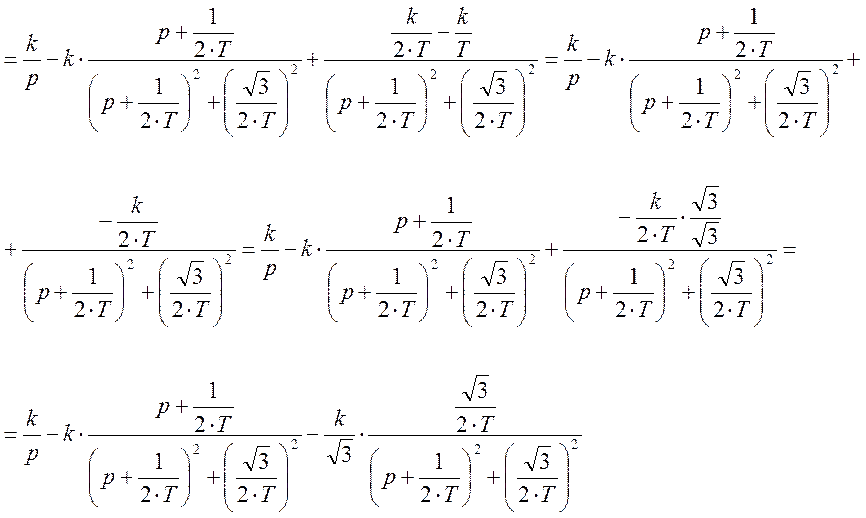
Так как по таблице обратных преобразований Лапласа:

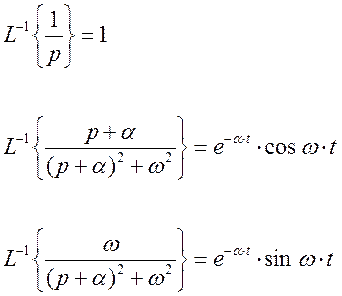
то дробь по Лапласу будет преобразована так.

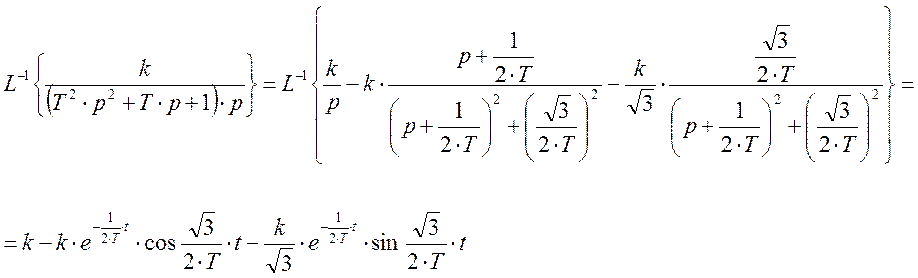
Подставим значения «Т» и «k» в получившееся выражение

2,2. Найдем время переходного процесса.

Из графика видно, что оно будет равно.

t_п=0,9

2,3. Определим перерегулирование, то есть максимальное отклонение регулируемой величины от установившегося значения, выраженное в процентах.

           

                                                                                                                                                                                                                              

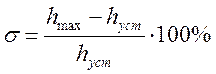
h_max можно определить как графически, так и аналитически.

Аналитически:

Найдем первую производную от исследуемой функции.

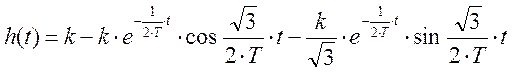
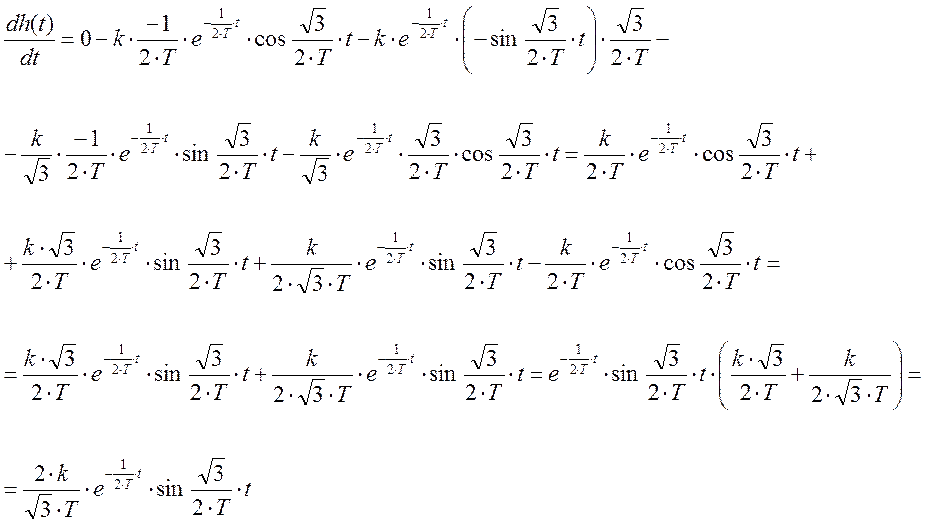
Приравняем ее к нулю и решим получившееся уравнение относительно t.

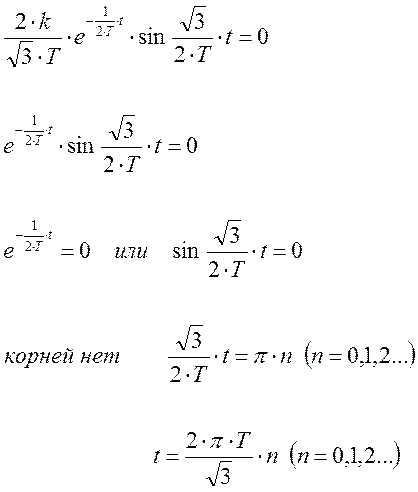
Тогда значение функции h(t) в данной точке будет равно.

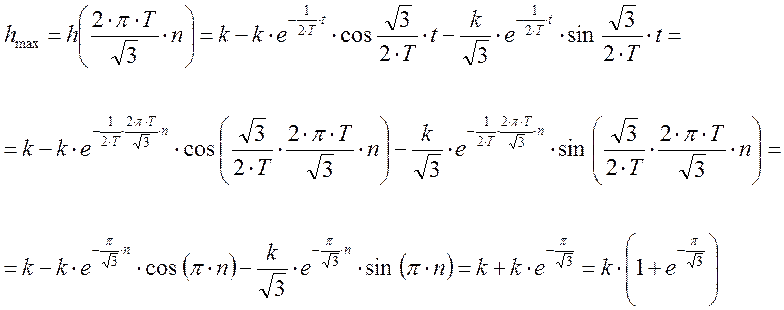
Подставив значение k можно определить h_max(t).

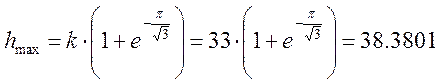
Графически:

Из графика видно, что максимальное амплитудное значение h(t) будет примерно равно.

h_max=38,4

Значит, перерегулирование будет равно.

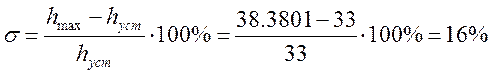
2,4. Найдем колебательность системы, то есть число колебаний регулируемой величины за время переходного процесса.

По графику видно, что за время переходного процесса происходит почти одно колебание, значит можно считать, что.

n=1.

2,5 Определим время нарастания регулируемой величины. (время необходимое для нарастания регулируемой величины до своего максимального значения).

Максимальное значение регулируемой величины будет h_max. Этому значению соответствует время, найденное по пункту 2.3, которое равно.

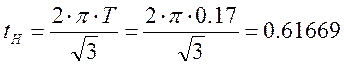
Это время можно было определить графически, посмотрев на графике переходного процесса, какому значению времени соответствует максимальное значение сигнала.

Оно также будет примерно равно.

2,6. Определим время первого согласования – это время, когда регулируемая величина первый раз достигает своего установившегося состояния.

Графически:

Графики переходного процесса и установившегося значения пересекаются в точке с координатами (0,4  : 33), то есть

Аналитически:

Для нахождения общей абсциссы пересечения графиков приравняем правые части следующих функций,

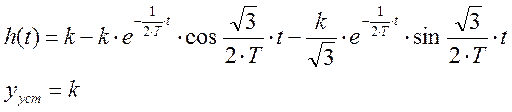
 а затем решим получившееся уравнение относительно t.

то есть

Значения, полученные аналитически и графически, совпадают.

3. Косвенные оценки качества. Они проводятся по амплитудно-частотной функции.

 - частотная форма передаточной функции.

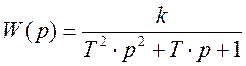
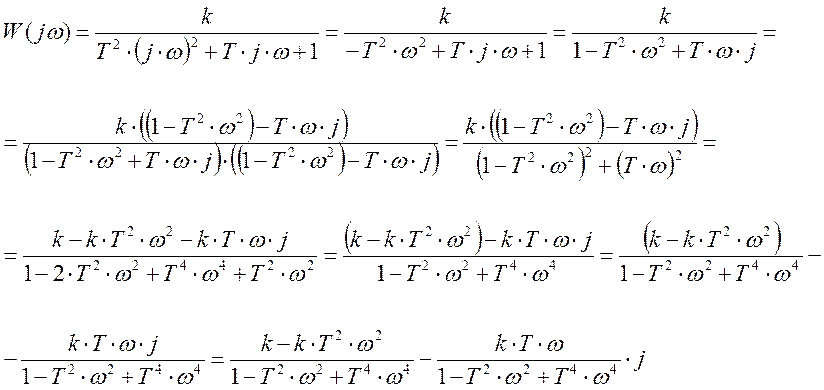
Тогда:

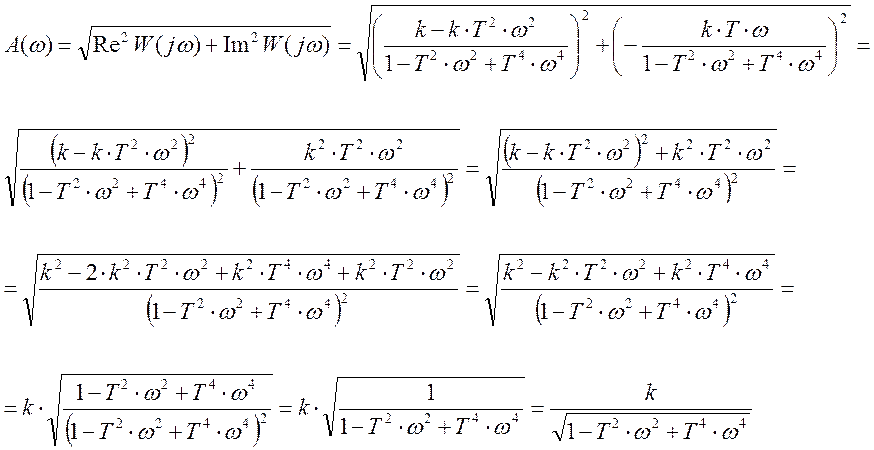
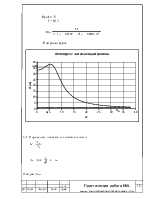
3,1. Определим  показатель колебательности.

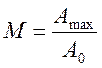
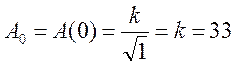
Найдем А_max.

Графически:

Тогда из графика видно, что эта величина достигает своего максимального значения, которое примерно равно.

Аналитически:

Найдем первую производную от исследуемой функции.

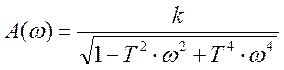
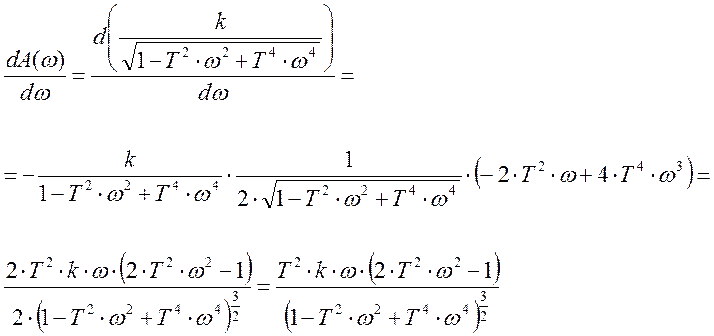
Приравняем ее к нулю и решим получившееся уравнение относительно w.

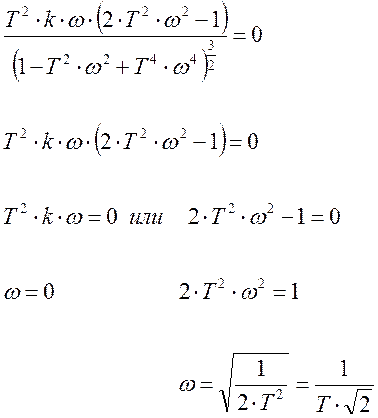
Тогда значение функции А(w) в данных точках будет равно.

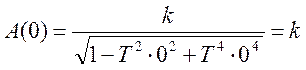
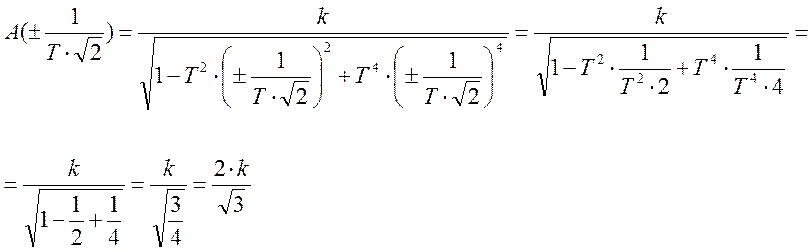
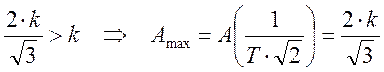
Подставив значение k можно определить А_max.

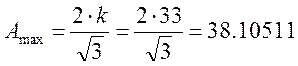
Тогда показатель колебательности будет равен.

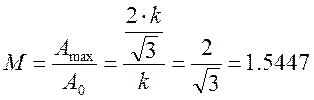
3,2. Найдем резонансную частоту – частота, в которой АЧХ достигает своего максимального значения.

Максимальное значение АЧХ величины будет А_max. Этому значению соответствует частота, найденная по пункту 3.1, которая равна.

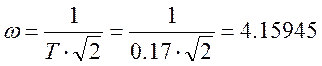
Эту частоту можно было определить графически, посмотрев на графике АЧХ, какому значению частоты соответствует максимальное значение сигнала.

Она также будет примерно равна.

3,3. Определим частоту среза – частота, в которой АЧХ достигает значение, равное 1.

Графически:

Графики функций А(w) и «1» пересекаются в точке с абсциссой равной:

Аналитически:

Для этого решим следующее уравнение относительно w.

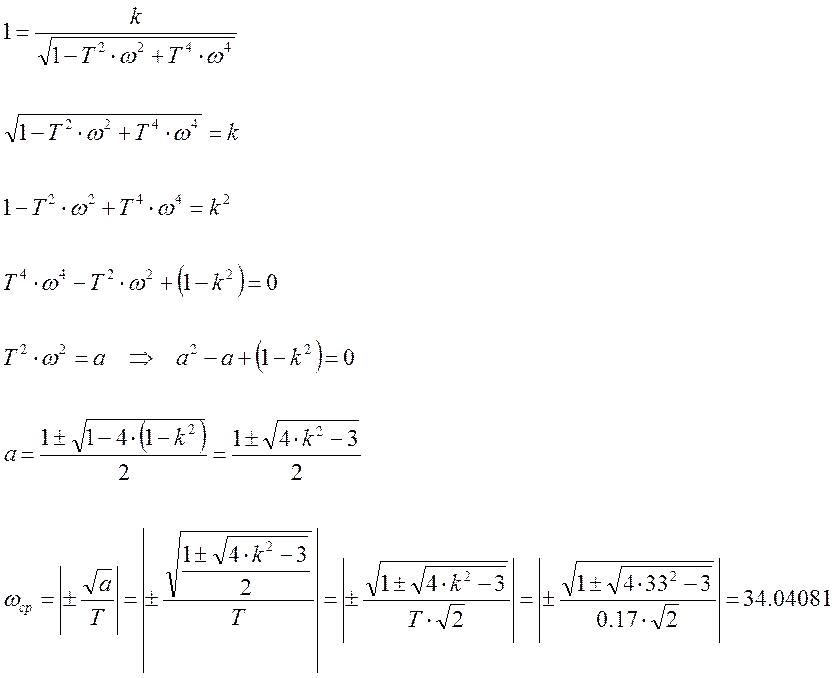
Таким образом, мы определили все требуемые величины.

Вывод: на основании проделанной работы, я научился определять устойчивость системы и оценивать ее качество, используя прямые и косвенные методы, а также строить графики переходных процессов систем автоматического регулирования, познакомился преобразованиями Лапласа.