Математическое описание линейных систем

1.  Методические указания и примеры выполнения заданий по курсовой работе

Задание 5. Математическое описание линейных систем

Пусть

Передаточная функция системы  – это отношение изображения по Лапласу сигнала на выходе к изображению по Лапласу сигнала на входе при нулевых начальных условиях.

Создадим стационарный линейный объект с именем w в пакете Matlab 

>> w = tf ([144 288], [1 15 62 48])

Transfer function:

144 s + 288

-----------------------s^3 + 15 s^2 + 62 s + 48

Чтобы перейти от передаточной функции к дифференциальному уравнению системы, нужно перейти из области изображений по Лапласу во временную область. Из (4.1)следует:

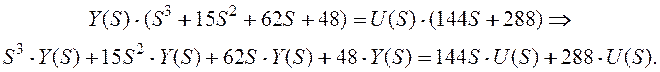
Для перехода во временную область воспользуемся формальными правилами:

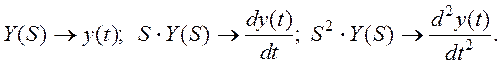
Тогда дифференциальное уравнение системы имеет вид

         (1.1)

Характеристическое уравнение системы определяется знаменателем передаточной функции

Один из корней уравнения можно найти подбором, это будет  а затем понизить порядок уравнения и решить его

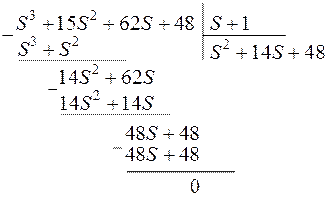
Итак,  тогда   

В пакете Matlab корни многочлена можно найти с помощью команды pole(w).

Matlab

>> pole(w)

ans =

-8.0000

-6.0000

-1.0000

Передаточная функция системы в форме нулей и полюсов имеет вид

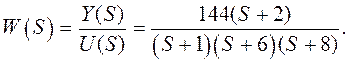
Получим разложение передаточной функции на сумму простых слагаемых

Найдем a, b, c :

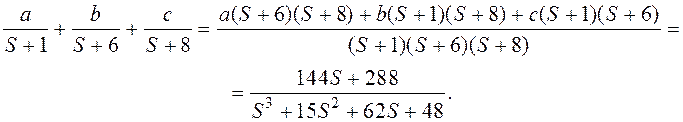
Следовательно,

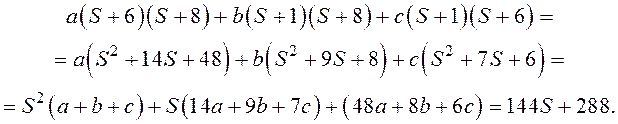
Получим систему уравнений:

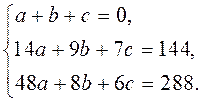
В результате решения данной системы уравнений получим         .

Импульсная переходная характеристика w(t) – это процесс изменения  сигнала на выходе при подаче на вход δ-функции. Ее можно найти в результате обратного преобразования Лапласа, примененного к каждому слагаемому передаточной функции.

В соответствии с таблицами соответствия 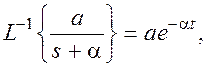 тогда

Matlab

>> ch=[144 288]

>> zn=[1 15 62 48]

>> [x]=residue(ch,zn)

x =

  -61.7143

   57.6000

    4.1143

Переходная характеристика h(t) – это процесс изменения сигнала на выходе системы при подаче на вход единичного ступенчатого воздействия. Преобразование по Лапласу 1(t) это

Для получения аналитической формы переходной характеристики дополним систему интегратором:

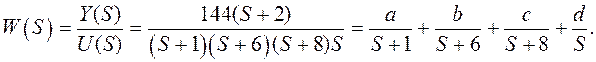
С помощью метода неопределенных коэффициентов аналогично найдем а = -4,114; b = -9,6; c = 7,714; d = 6.

Matlab 

>> ch=[144 288]

>> zn=[1 15 62 48]

>> [c]=residue(ch,[zn,0])

c =

7.7143

-9.6000

-4.1143

6.0000

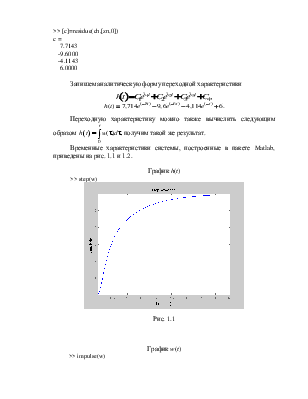
Запишем аналитическую форму переходной характеристики

Переходную характеристику можно также вычислить следующим образом 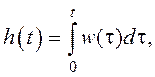 получим такой же результат.

Временные характеристики системы, построенные в пакете Matlab, приведены на рис. 1.1 и 1.2.

График h(t)

>> step(w)

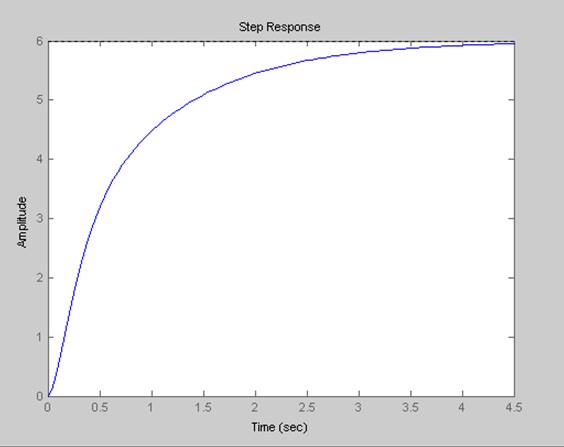
Рис. 1.1

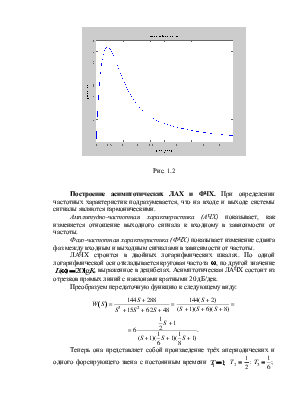
График w(t)

          >> impulse(w)

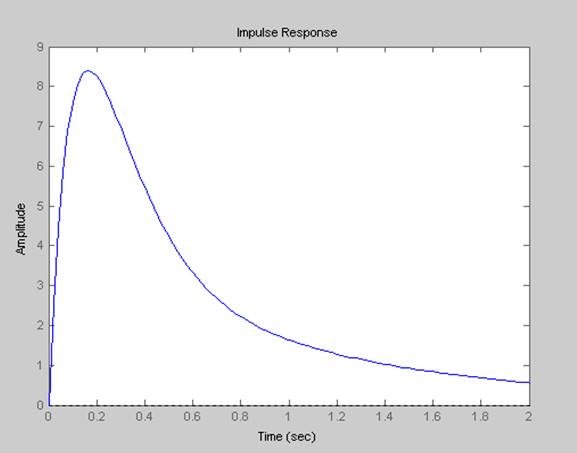
Рис. 1.2

Построение асимптотических ЛАХ и ФЧХ. При определении частотных характеристик подразумевается, что на входе и выходе системы сигналы являются гармоническими.

Амплитудно-частотная характеристика (АЧХ) показывает, как изменяется отношение выходного сигнала к входному в зависимости от частоты.

Фазо-частотная характеристика (ФЧХ) показывает изменение сдвига фаз между входным и выходным сигналами в зависимости от частоты.

ЛАЧХ строится в двойных логарифмических шкалах. По одной логарифмической оси откладывается круговая частота , по другой значение , выраженное в децибелах. Асимптотическая ЛАЧХ состоит из отрезков прямых линий с наклонами кратными 20 дБ/дек.

Преобразуем передаточную функцию к следующему виду:

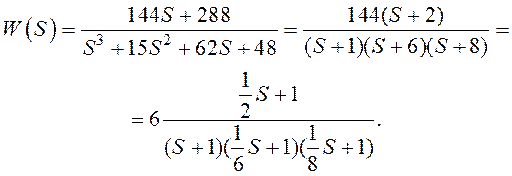
Теперь она представляет собой произведение трёх апериодических и одного форсирующего звена с постоянным времени     Коэффициент усиления К = 6. Сопрягающие частоты звеньев равны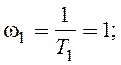    

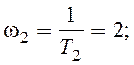
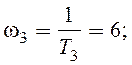
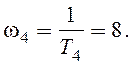
Далее необходимо правильно разметить оси, и отметить на оси w сопрягающие частоты. ЛАЧХ приведена на рис. 1.3, а.

Так как интегрирующие звенья отсутствуют, то первый наклон в области низких частот будет нулевой. Он идёт параллельно оси частот на уровне 20 lgK до первой сопрягающей частоты w₁. Эта частота относится к апериодическому звену. Следовательно, наклон изменится на -1. Этот наклон будет идти до сопрягающей частоты w₂. Так как эта частота относится к форсирующему звену, то наклон изменится на +1 и станет нулевым, ЛАЧХ параллельна оси частот. После частоты w₃ наклон изменится на (-1) и будет продолжаться до w₄.  После частоты w₄  он изменится ещё на (-1) и станет равным (-2). Частота, при которой частотная характеристика пересечёт ось частот, называется частотой среза, w_ср = 12 рад/с.

Фазочастотная характеристика (рис. 1.3, б) построена в соответствии с выражением

Значения каждого из слагаемых определяются приближенно для значений ,  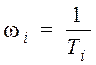. В этих точках  

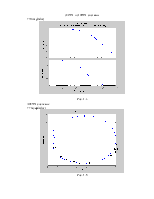
В пакете Matlab для построения ЛАЧХ и ЛФЧХ используется команда bode(w), а для построения АФЧХ команда nyquist(w). Соответствующие характеристики приведены на рис. 1.4 и 1.5.

а

б

Рис. 1.3

ЛАЧХ и ЛФЧХ системы

>>margin(w)                                         

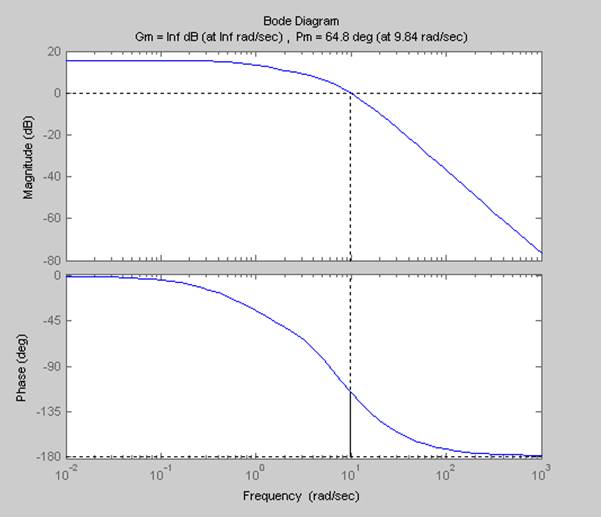
Рис. 1.4

АФЧХ системы:

>> nyquist(w)

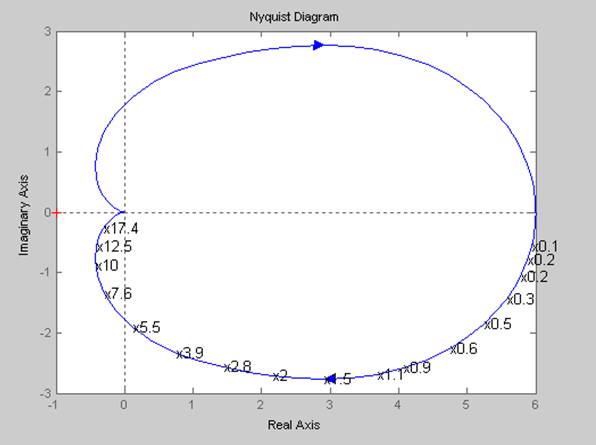
Рис. 1.5

Кроме входных и выходных переменных при описании систем выделяют переменные x, связанные с внутренней структурой устройства – переменные состояния. Тогда систему можно описать с помощью уравнений состояния.