Строительство и архитектура \ Организации строительства

Компоновка конструктивной схемы каркаса здания. Расчёт поперечной рамы здания. Проверка местной устойчивости верхней и нижней части колонны, страница 7

Подкрановая ветвь:

Задаваясь коэффициентом , которому, согласно таблице 2 [3], соответствует гибкость , находим ориентировочную площадь сечения:

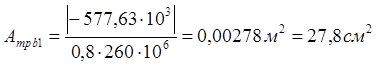
Проектируем ветвь в виде сварного двутавра. Его высоту для обеспечения устойчивости колонны из плоскости действия изгибающего момента определяем из условия:

Рисунок 16 – Сечение двутавра

Общая площадь трёх листов двутавра:

Конструктивно принимаем =20 мм, =12 мм. Ширина полок:

Условие выполнено.

Наружная ветвь:

Требуемая площадь наружной ветви при том же коэффициенте продольного изгиба:

Рисунок 17 – Сечение наружной ветви

Принимаем сечение ветви из двух равнополочных уголков и листа общей площадью:

где – площадь одного уголка,

, – ширина и толщина листа:

По сортаменту [1] принимаем уголок №20 200×18.

Определяем геометрические характеристики ветвей:

1. Сечение подкрановой ветви:

Моменты инерции:

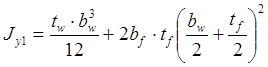
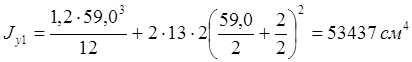
Радиусы инерции:

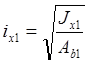
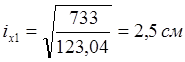
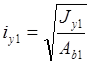
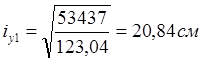
2. Сечение наружной ветви:

Координата центра тяжести сечения относительно внешней грани листа:

где – площадь листа:

– площадь всей ветви:

=+2

– характеристика уголка,

Моменты инерции:

- в плоскости:

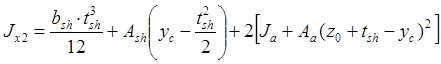
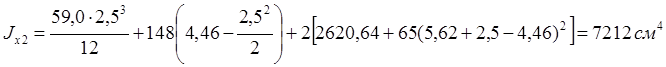
- из плоскости:

Радиусы инерции:

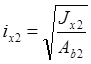
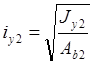
3. Сечение колонны в целом:

Координата центра тяжести сечения относительно центра оси двутавра:

– площадь поперечного сечения всей подкрановой части:

Момент инерции:

Радиусы инерции:

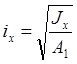
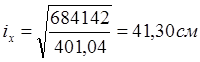
Проверка устойчивости ветвей колонны:

- подкрановая ветвь:

Уточнение значения продольного усилия:

Гибкость рамы:

– расстояние между узлами решётки:

– высота траверсы в месте сопряжения верхней части ступенчатой колонны с нижней частью, ;

– высота нижней части колонны, ;

– количество панелей верхней части колонны, =8

Определим гибкость из плоскости рамы:

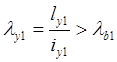
Максимальная условная гибкость:

Коэффициент продольного изгиба:

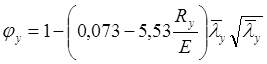
Напряжение:

- наружная ветвь:

Аналогично находим характеристики для наружной ветви:

Гибкость рамы:

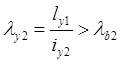
Коэффициент продольного изгиба:

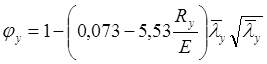
Напряжение:

Следовательно устойчивость отдельных ветвей подкрановой части обеспечена.

3.6 Расчёт базы колонны

Т.к. ширина нижней части колонны ≥ 100 см, то в пролёте принимаем базу колонны раздельного типа. Каждая из ветвей рассчитывается на уточнённое значение продольной силы, в которую уже включены моменты и расстояния до центра тяжести, поэтому каждую из ветвей можно рассматривать центрально сжатой. Отличается база от центрально сжатой колонны только своим конструированием.

Траверсы расположены вдоль оси действия момента и плита базы вытягивается в этом же направлении.