Компоновка конструктивной схемы каркаса здания. Расчёт поперечной рамы здания. Проверка местной устойчивости верхней и нижней части колонны, страница 5

Суммарная эпюра значений моментов на левой стойке (рисунок 10г):

Суммарная эпюра значений моментов на правой стойке (рисунок 10г):

Эпюра Q (рисунок 10д):

Поперечная сила на правой стойке:

Сумма поперечных сил должна равняться сумме всех горизонтальных нагрузок:

2.3.4 Расчёт на вертикальную нагрузку от мостовых кранов

Расчёт проводится при расположении тележки крана у левой стойки. Основная система и схема загружения приведены на рисунке 11а.

Проверка возможности считать ригель абсолютно жёстким выполняется по формуле:

где J_P=20 – момент инерции ригеля

Условие выполняется, т.о. можно считать ригель абсолютно жёстким.

Каноническое уравнение для определения смещения плоской рамы:

Момент и реакция от смещения верхних узлов на Δ=1 (рисунок 11б) определяется с помощью таблицы 12.4.

Моменты и реакции на левой стойке от нагрузки (рисунок 11в):

М – максимальная нагрузка от крана

Усилия на правой стойке получаем аналогично, умножая усилия левой стойки на отношение :

Реакция верхних концов стоек:

Смещение плоской рамы:

Крановая нагрузка линейная, поэтому .

При жёсткой кровле  определяется:

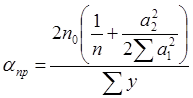
где n – число рам в блоке, n=13;

 – расстояние между симметрично расположенными относительно середины блоками рамы:

=72²+60²+48²+36²+24²+12²=13104;

 – расстояние между рамами, стоящими вторыми от торцов здания, =60м;

 – число колёс крана на одной нитке подкрановой балки, =2;

– сумма координат линий влияния, =1,15м

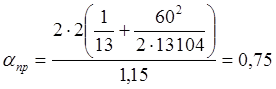
Смещение с учётом пространственной работы:

Эпюра моментов  от фактического смещения рамы с учётом пространственной работы показана на рисунке 11г, а суммарная эпюра + –  на рисунке 11д.

Эпюра Q (рисунок 10е) свидетельствует о правильности расчёта (поперечные силы в верхних и нижних частях стоек практически одинаковы).

Разница в значениях нормальных сил (рисунок 11ж) с левого и правого концов ригеля получились за счёт передачи горизонтальных сил на соседние рамы.

 

Рисунок 11 – К расчёту рам на вертикальную нагрузку

от мостовых кранов

2.3.5 Расчёт на горизонтальные воздействия от мостовых кранов

Основная система, эпюра М₁, каноническое уравнение, коэффициент  такие же как при расчёте на вертикальную нагрузку от мостовых кранов. Моменты реакции в основной системе от силы Т:

Смещение верхних концов с учётом пространственной работы:

 

Рисунок 12 – Эпюры усилий от горизонтальных воздействий крана

Проверка правильности решения:

Скачёк на эпюре Q 6,7+4,2=10,9кН примерно равен силе Т=10,5кН, а на правой стойке поперечные силы в верхней и нижней частях равны 3,49кН.

3. РАСЧЁТ И КОНСТРУИРОВАНИЕ КОЛОННЫ

Верхняя часть колонны проектируется в виде симметричного сварного двутавра. Расчётные значения усилий (смотри таблицу 2) равны:

- для верхней части колонны в сечении 1-1 М_max=-440,44 кН·м, соответствующее ему усилие N_соотв.=-370,69 кН;

- для нижней части колонны в сечении 3-3 М_max=-257,93 кН·м, соответствующее ему усилие N_соотв.=-528,76 кН (изгибающий момент догружает подкрановую ветвь);

- в сечении 4-4 М_max=557,33 кН·м, соответствующее ему усилие N_соотв.=-528,76 кН (изгибающий момент догружает наружную ветвь);

- Q_max в сечении 4-4 составляет -22,65 кН.

Соотношение жесткостей

3.1 Определение длины в плоскости и из плоскости рамы

Колонна работает на сжатие с изгибом. Расчётные длины для верхней и нижней частей колонны в плоскости рамы определяем по формулам:

 – расчётная длина верхней части колонны;

 – расчётная длина нижней части колонны;

– высоты верхней и нижней части колонны,

 – коэффициент расчётной длины, =, где n – отношение жёсткости верхней и нижней части колонны:

– коэффициент, учитывающий соотношение продольных сил:

=

=

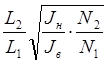
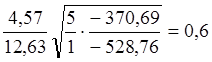
По таблице 2 Приложения 12 [2], которая содержит коэффициент приведения  для одноступенчатых колонн с верхним концом, закреплённым только от поворота, интерполируя, получим значение  и вычислим значение :