Исследование системы регулирования температуры системы отопления, страница 2

.

Выделим вещественную и мнимую части:

,

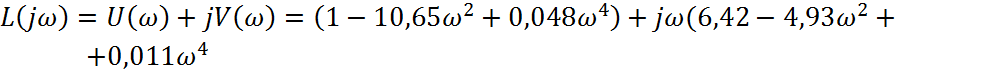где        - вещественная часть;

 - мнимая часть.

Используя программу MathCAD, построим годограф Михайлова:

Рисунок 6 – Годограф Михайлова

Рисунок 7 – Годограф Михайлова в большем масштабе

Из графика видно, что система является устойчивой, потому что годограф Михайлова системы пятого порядка при изменении частоты от нуля до бесконечности последовательно проходит против часовой стрелки по всем квадрантом, начиная с вещественно оси, и в пятом квадранте уходит в бесконечность.

1.7 Построение переходного процесса системы

Переходная функция - это реакция системы на ступенчатое входное воздействие.

Для того, чтобы построить переходный процесс, используем обратное  преобразование Лапласа от функции вида  .

Передаточная функция САУ имеет вид:

 .

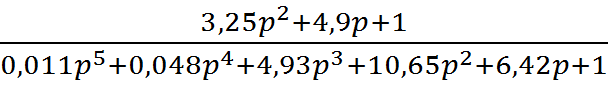График переходного процесса построим программой Маthcad.

Переходная функция:

 

 

 .

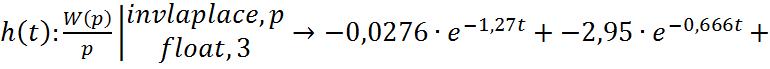
Рисунок 8 – График переходного процесса

Из графика переходного процесса видно, что система устойчива.

Определяем прямые оценки качества системы:

Установившееся значение  .

Время переходного процесса, (время, за которое система входит в 5%-ти процентную трубку устойчивости и больше ее не покидает)  .

Время нарастания  регулируемой величины (время за которое регулируемая величина достигает максимального значения) .

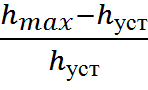
Перерегулирование (максимальная динамическая ошибка), определяемая выражением   , невозможно найти, так как .

Время первого согласования (время, когда регулируемая величина достигает первый раз своего установившегося значения)  .

Колебательность (число колебаний за время колебаний за время колебательного процесса)  n=0.

1.8 Построение амплитудно-частотной характеристики системы

Для построения графика АЧХ необходимо в передаточной функции САУ заменить , получим:

 

.

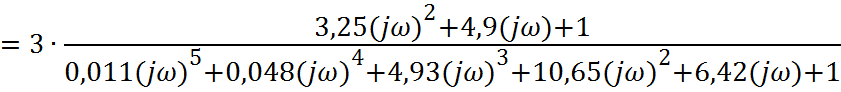АЧХ рассчитывается по формуле:

.

Построим амплитудно-частотную характеристику в Mathcad

Рисунок 9 – График амплитудно–частотной характеристики

Рисунок 10 – График АЧХ в большем масштабе

Определим косвенные оценки качества системы:

Резонансная частота (частота при которой АЧХ достигает своего максимального значения)

Максимальное значение амплитуды  .

Частота среза (частота при которой амплитудно-частотная характеристика достигает значения 1)  .

Полоса пропускания    вычисляется при .

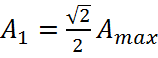Показатель колебательности    .

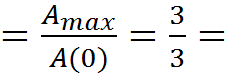
1.9 Построение логарифмической амплитудно-частотной характе-

ристики и логарифмической фазо-частотной характеристики

График ЛАЧХ строим по формуле:

.

Рисунок 11 – График логарифмической амплитудно-частотной характериc-

                       тики

График ЛФЧХ строим по следующей формуле:

 .

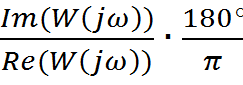Рисунок 12 – График логарифмической фазо-частотной характеристики

Запас устойчивости по фазе .

Запас устойчивости по амплитуде найти невозможно, так как ЛФЧХ не пересекает -180°.

Аппроксимируем ЛАЧХ, изображённую на рисунке 11:

+40 Дб/дк

0 Дб/дк

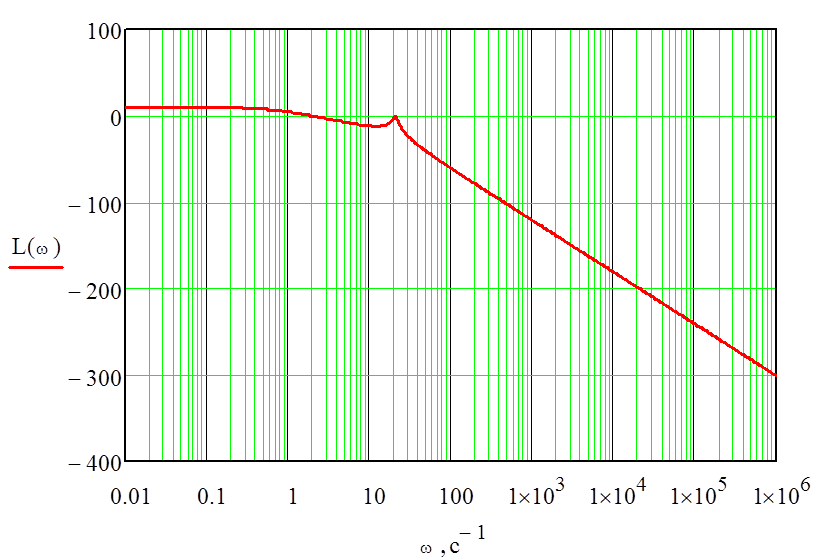
Рисунок 13 – Аппроксимация ЛАЧХ

Из рисунка видно, что передаточная функция имеет вид:

.

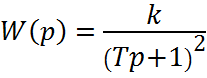Для того, чтобы записать полученную передаточную функцию системы в численном виде, необходимо рассчитать Т, по формуле:

 .

Частота  находится из рисунка 13. Для того чтобы её определить, нужно опустить перпендикуляр с точки пересечения аппроксимированных участков.

Таким образом, из рисунка видно, что .

Следовательно, передаточная функция системы в численном виде будет иметь вид:

 .

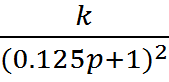2 АНАЛИЗ НЕЛИНЕЙНОЙ СИСТЕМЫ

2.1 Фазовый портрет системы

 

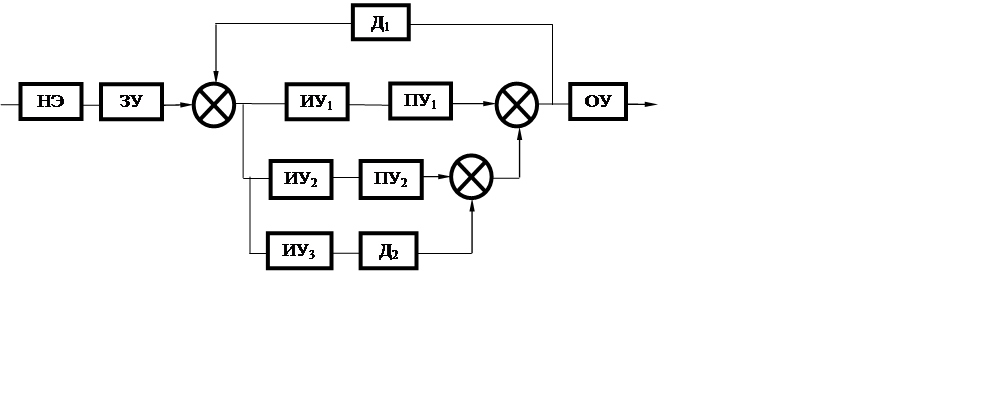Рисунок 14 – Структурная схема системы с нелинейным элементом.

Отрезок (-1,5, 1,5) называется шириной петли гистерезиса, в ряде случаев ширина петли должна быть большой и это является полезным для системы, а в ряде случаев петля гистерезиса приводит к нежелательным последствиям, поэтому ее стремятся уменьшить. Приведенной характеристикой обладают электромагнитные реле и электромагниты. Обычно для  электромагнитного реле  величина «1,5» называется порогом срабатывания, а величина «-1,5» -  порогом отпускания.

 

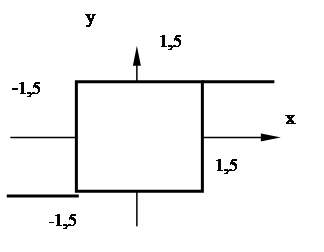Рисунок 15 – Релейная статическая характеристика с гистерезисом

По правилам преобразования структурных схем преобразуем нелинейную систему.

 

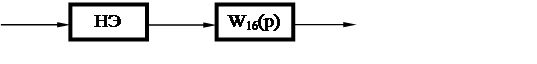Рисунок 16 - Структурная схема нелинейной системы после преобразова-

                       ний

Т.е. передаточная функция линейной части системы имеет вид:

 .

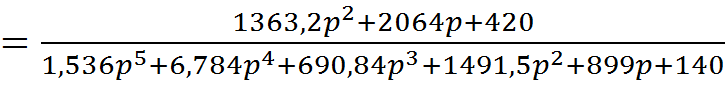Передаточная функция есть  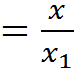 или ,

где      - передаточная функция линейной системы;

Подставляя в эту формулу значение передаточной функции получим:

  .

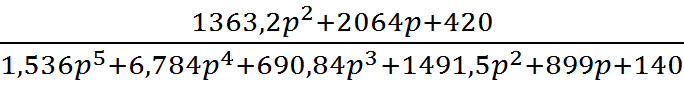
Приведенную формулу можно записать в виде:

.

Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.

Введем замену  и исключим из правой части уравнения производную:

.

Для того чтобы построить фазовый портрет, необходимо, чтобы степень числителя и знаменателя не превышала вторую степень, поэтому элементы выше второй степени исключаем. Тогда получим:

,

.

Так как в качестве нелинейного элемента используется реле с гистерезисом со статической характеристикой, представленной на рисунке 14, то подставляя значение  для двух участков, получим систему:

;

;

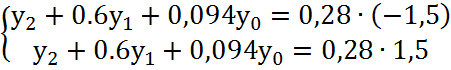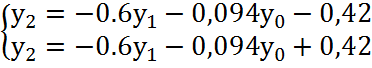Создадим матрицу для решения дифференциального уравнения.

В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицы для трех начальных условий:

; ; .

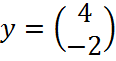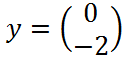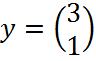Возьмем количество точек равным 1000 и конечное время интегрирования 100, матрица решений запишется в виде:

,

.

Построим фазовый портрет:

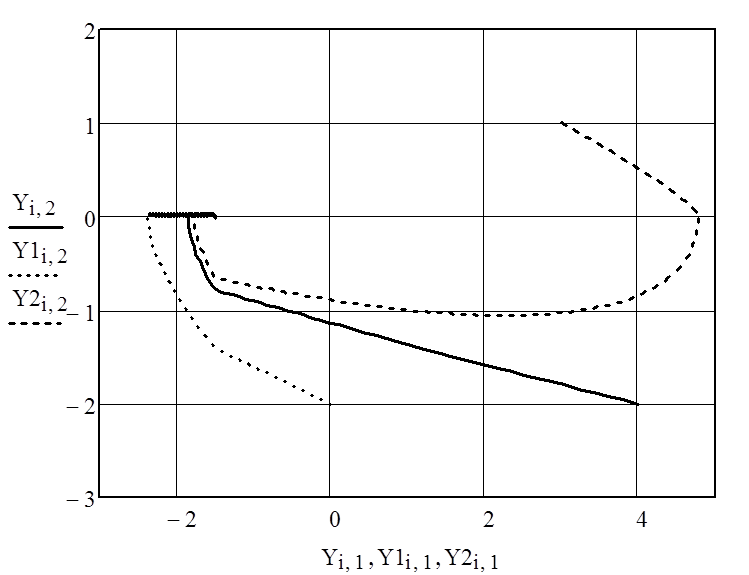
Рисунок 17 – Фазовый портрет системы

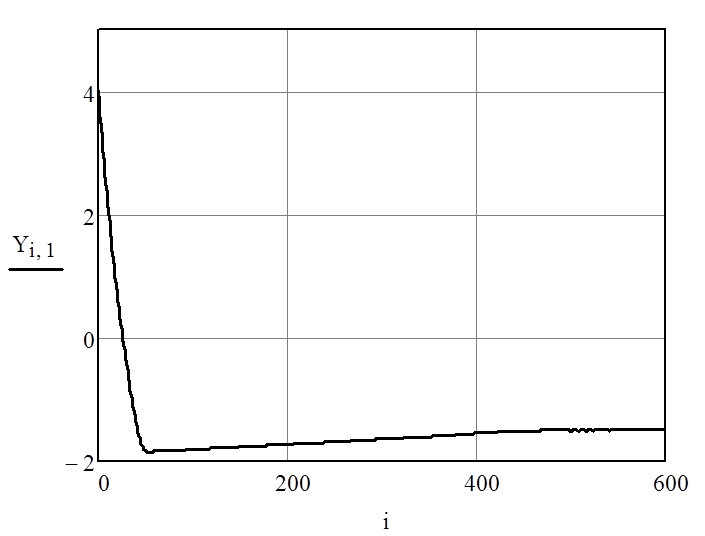
Рисунок 18 – Переходный процесс системы

ЗАКЛЮЧЕНИЕ

В данной курсовой работе была рассмотрена системы регулирования температуры системы отопления. В ходе исследования были построены функциональная и структурная схемы системы. Исследована линейная  часть системы.

При исследовании линейной части системы была проведена проверка на устойчивость по критериям Гурвица и Михайлова. Были определены прямые оценки качества системы управления (время переходного процесса, перерегулирование, колебательность,  время нарастания регулируемой величины, время первого согласования) по построенному графику переходного процесса и косвенные оценки качества системы управления (резонансная частота, показатель колебательности, частота среза, полоса пропускания) по АЧХ .

При исследовании нелинейной части была упрощена структурная схема и построены графики фазового портрета и переходного процесса нелинейной системы.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.  Айзерман М.А. Теория автоматического регулирования. 2-е издание. / М.А. Айзерман. – М.: Наука, 1966. – 452 с.

2.  Бесекерский В.А. Теория систем автоматического регулирования / 
В.А. Бесекерский, Е.П. Попов. – М.: Профессия, 2003. – 380 с.

3.  Воронов А.А. Основы теории автоматического регулирования. / А.А. Воронов.  – М.: Высшая школа, 1977. – 519 с.

4.  Зайцев Г. Ф. Теория автоматического управления и регулирования. — 2-е изд., перераб. и доп. / Г.Ф. Зайцев. -  К: Выща шк. Головное изд-во, 1989.— 431 с. - ISBN 5-11-000225-8.

5.  Ким Д.П. Теория автоматического управления: Линейные системы. Т.1 / Д.П. Ким. – М.: - Физматлит, 2003. – 288 с. – ISBN 5-9221-0379-2.

6.  Кошарский Б.Д. Автоматические приборы и регуляторы. / Б.Д. Кошарский, В.А. Бек.  – М.: Машиностроение, 1964. – 704 с.

7.  Лазарева Т.Я. Теория автоматического управления: Учеб.-метод. пособие / Т.Я. Лазарева, Ю.Ф. Мартемьянов, В.Ю. Харченко. - Тамбов: Изд-во Тамб. гос. техн. ун-та, 2006. – 56 с.

8.  Летов А.М. Устойчивость нелинейных регулируемых систем. / А.М.  Летов. – М.: Физматгиз, 1962. – 315 с.

9.  Поспелов Г.С. Импульсные системы автоматического регулирования. / Г.С. Поспелов. – М.: Машгиз, 1950. – 256 с.

10.   Пугачев В.С. Основы автоматического регулирования. / В.С. Пугачев. – М.: Наука, 1974. – 720 с.