Конструктивные решения. Расчет плиты покрытия. Определение положения нейтральной оси сечения плиты. Расчетные усилия в плите, страница 3

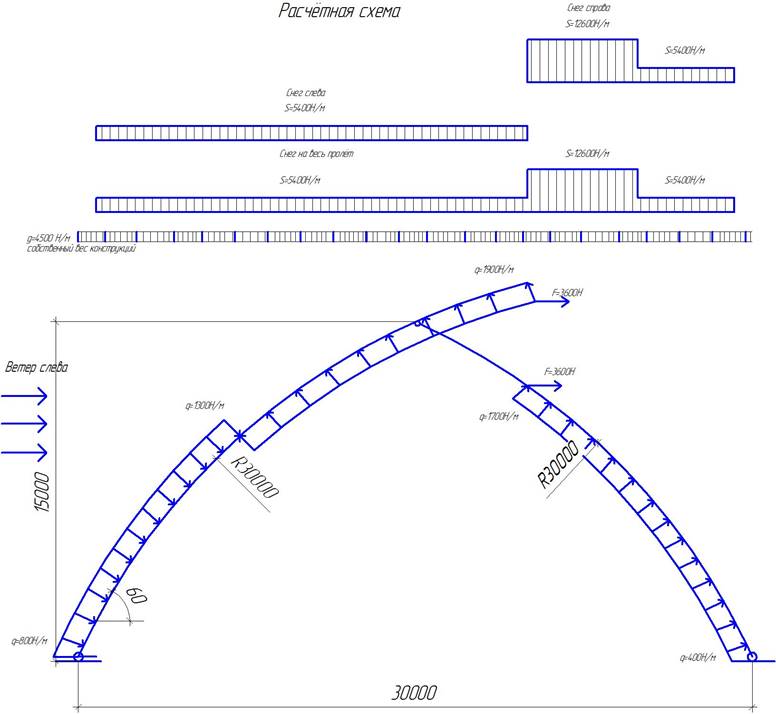
Рисунок 2.1. Расчетная схема арки

2.4. Расчётные сочетания усилий.

Расчетные эпюры изгибающих моментов, эпюры продольных и поперечных сил приведены на рисунках

Расчётным сечением является сечение № 12 при загружении снег справа по схеме Г1 и ветре справа.

М_расч= + 296 кН м

N_соотв= - 138,1кН.

Расчётным сечением по отрицательному изгибающему моменту является сечение № 12 при загружении снег слева по Г1 и ветер слева.

М = -140,4кНм

N_соотв= -137,3 кН.

Максимальное значение продольной силы в ключевом шарнире при загружении кратковременной снеговой нагрузкой на весь пролёт и ветру с права

N_кл=-122 кН

Q_соотв=42,11 кН

Максимальное значение продольной силы в левой опоре арки равно при загружении кратковременной снеговой нагрузкой на весь пролёт и ветру справа

N_0л= - 240кН

Q_соотв= - 19,2 кН

Максимальное значение продольной силы в правой опоре арки равно при загружении кратковременной снеговой нагрузкой на весь пролёт и ветру справа

N_0п= - 264кН

Q_соотв= + 10,9 кН

2.5. Предварительный подбор сечения арки.

Материал арки – сосновые доски по ГОСТ 24454 – 80 первого и второго сорта.

Расчётные характеристики материала определены в соответствии с п.3 [2].

При толщине слоёв сечения арки δ= 33 мм ( R/a= 30000/33 = 909 > 500 ) с высотой сечения арки h_a>50 см (по конструктивным требованиям - h_a=l/40=30/40=0,75м), расчётные сопротивления для сосны 2-го сорта будут равны:

R_u=R_c=R_см=R_табл.· m_б =15·0,8=12 МПа

Назначение предварительных размеров сечения арки.

Требуемое значение момента сопротивления сечения арки:

W_тр=а·М/ξ·R_c=1,05·296/0,8·12·10³=0,0324 м³

где М – максимальное по абсолютной величине значение изгибающего момента в арке;

x =0,8 - предварительное значение коэффициента, учитывающего влияние дополнительного изгибающего момента от продольной силы при расчёте по деформированной схеме.

R_c - расчётное сопротивление древесины сжатию;

а – коэффициент, учитывающий долю нормальных напряжений от продольной силы:

a=1+N · h/6M=1+(138·0,75)/(6·296)=1,05

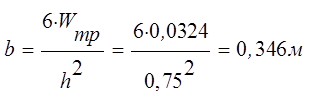
h_опт===0,75 м

Принято сечение bхh = 360х759(23х33) с толщиной слоя δ_сл=33 мм.

Так как b=360мм принимаем сечение состоящее из двух ветвей по 180мм 

2.6. Расчёт элементов арки по предельным состояниям.

2.6.1. Проверка прочности принятого сечения при положительном изгибающем моменте и окончательная компоновка сечения арки.

М_расч=296 кНм ; N_соотв=-138,1 кН ; N_кл.=-122кН

F_расч=b×h=0,36·0,759=0,273 м² W_расч=bh²/6=0,36·0,759²/6=0,034м³

Проверяем прочность сечения по формуле (28) [2]:

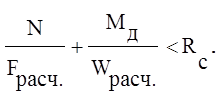
где 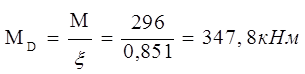 - изгибающий момент, определённый по деформированной схеме

 

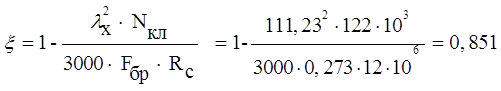
ξ - коэффициент учитывающий дополнительный момент от продольной силы

λ_x=L₀/r_x=24,36/0,219=111,23;

r_x=0,289×h=0,289·0,759=0,219м

L₀=0,58×S=0,58·42=24,36 м

R_u=R_c=R_см=R_табл.·m_б·m_п·m_в=15·0,8=12 МПа

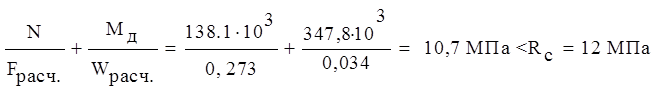
условие прочности выполняется

Принятые размеры поперечного сечения арки – 360х759 мм удовлетворяют условию прочности. Поперечное сечение показано на рисунке 2.2

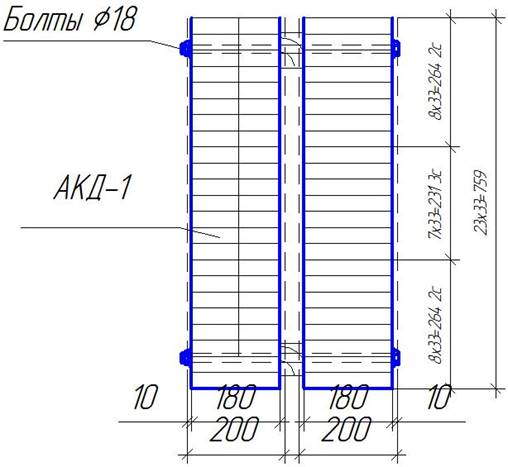
Рисунок 2.2 - Поперечное сечение арки.

2.6.2. Проверка прочности принятого сечения арки при

 отрицательном изгибающем моменте.

М=-140 кНм ; N_соотв=-137,3 кН ; N_кл.=-122 кН.

Как видим величина отрицательного изгибающего момента в нашем случае в двое меньше положительного, продольная же сила изменилась не значительно и в меньшую сторону. Необходимость осуществлять проверку прочности сечения при отрицательном М отсутствует.

2.6.3. Проверка устойчивости арки в плоскости кривизны

как центрально сжатого стержня.

Расчётное усилие N₀=-264 кН

Согласно п. 6.27 [2] проверку производим по формуле:

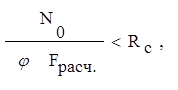
где φ_м - коэффициент продольного изгиба, определяемый по формуле (8) [2].

Устойчивость арки в плоскости кривизны обеспечена.

2.6.4. Проверка устойчивости плоской формы деформирования арки.

При  действии  максимального  положительного изгибающего момента.

При действии положительного изгибающего момента сжатой является верхняя кромка арки, к которой прикрепляются плиты покрытия.

=3,6кН

Расстояния между рабочими раскреплениями кромки составляет 488 – 524 мм, то есть L_р=0,5 м. Растянутая кромка на такой длине не имеет закрепления, значит, проверка устойчивости производиться по формуле (33) [2]: