Конструктивные решения. Расчет плиты покрытия. Определение положения нейтральной оси сечения плиты. Расчетные усилия в плите, страница 2

Изгибающие моменты:

Поперечные силы:

Проверка плиты на прочность

Проверка нижней обшивки на растяжение (см. п.4.24 [1]).

 - условие выполняется.

3.7.2 Проверка верхней сжатой обшивки на устойчивость по п.4.26 [1]:

Так как в нашем примере , то  определяется по формуле:

.

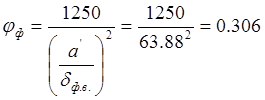Так как проверка не выполняется, принимаем толщину фанеры 10мм

Так как в нашем примере , то  определяется по формуле:

.

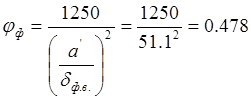Проверка плиты на сосредоточенную силу

Дополнительно верхняя фанерная обшивка плиты проверяется на местный изгиб от сосредоточенного груза Р=1000 Н с коэффициентом перегрузки n=1,2

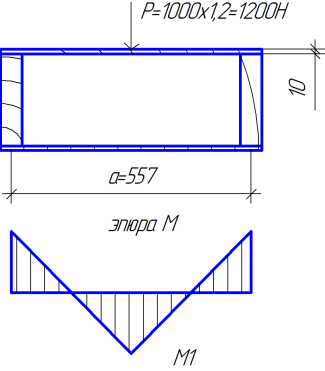
Рисунок 1.3 Расчётная схема обшивки на местный изгиб при ширине расчётной полосы b`_ф.в.=1,0 м по схеме приведённой на рисунке 4.3.

M₁=76,65 Н∙м;

16,67 см³=16,67∙10^-6 м³;

4.59∙10⁶ Па=4,59 МПа < R_фи∙m_н=5,85∙1,2=7,02 МПа.

Проверка прочности клеевого шва между верхней обшивкой и продольными ребрами на скалывание

Здесь

Проверка на скалывание древесины ребер по нейтральному слою согласно п.4.10 [1]:

Расчет плиты на жесткость (прогиб)

В соответствии с п.4.33 и п.4.34 [1] прогиб плиты должен определяться с учетом деформаций сдвига по формуле:

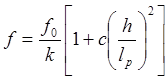, где ;

k=1, т.к. высота панели постоянна, согласно п.4.3 и табл.3 прил.4 [1];

, согласно табл.3 прил.4 [1];

=1,0 для постоянного сечения;

.

Коэффициенты k, с, β, γ определяются по таблице 3 приложения 4 [1] как для балки двутаврового сечения постоянной высоты с шарнирными опорами и линейно-распределенной нагрузкой.

Полный прогиб плиты равен:

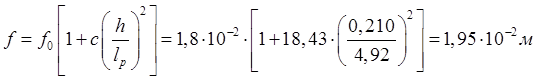
Относительный прогиб составляет:

, то есть не превышает допустимой величины (см. п.10.7, табл.19 [2]).

Таким образом, плита покрытия удовлетворяет требованиям прочности и жесткости.

       2. Расчет и конструирование трехшарнирной

деревянной клееной стрельчатой арки.

2.1. Определение геометрических размеров стрельчатой арки.

Расчетный пролет: L= 30 м.

Стрела подъема: f=15 м.

Радиус кривизны арки:

R=30м

2.2. Определение нагрузок на арку.

Нормативная нагрузка от собственного веса арки составит:

, где ,

 - коэффициент собственного веса арки.

Расчетная нагрузка от собственного веса арки составит:

, где  - коэффициент надежности по нагрузке.

Расчетная нагрузка от веса покрытия составит:

Расчетная нагрузка от собственного веса:

Расчетная снеговая нагрузка приходящая на каждый конечный элемент арки соответствующая первому варианту загружения:

, где  - коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие .

где  - давление скоростного напора ветра для г.Омск (2-й ветровой район);

 - коэффициент, учитывающий изменение ветровой нагрузки по высоте;

- коэффициент, учитывающий направление действия и интенсивность ветровой нагрузки;

 - шаг несущих конструкций.

Расчетная ветровая нагрузка:

где  - коэффициент надежности по ветровой нагрузке [1].

Таблица 2.1 – Значение угла α и координаты точек.

№ сеч	x	z	угол
1	0	0	66,00
2	1,58	3,1	60,00
3	2,79	5	54,00
4	7,13	10	43,00
5	12,76	14,1	30,00
6	15	15	20,00
7	17,23	14,1	30,00
8	27,21	5	54,00
9	22,87	10	43,00
10	20	12,4	41,00
11	20	17	15,00
12	25,05	7,79	48,00
13	28,42	3,1	60,00
14	30	0	66,00

2.3. Статический расчет арки.

Статический расчет выполнялся методом конечных элементов в перемещениях, реализованном в вычислительном комплексе “SCAD”. Расчетная плоская схема, по которой выполнялся расчет.