Статистика. Моду и медиана стажа рабочих завода. Оценка существенности коэффициента корреляции

Кафедра Экономики ГА

СТАТИСТИКА НА ВТ

Курсовая работа

ТЕМА: «»

Приняла:

Н.И. Степанова  ^{( ф. и. о.)}

_______________

^{(дата, подпись)}

Выполнил студент

_______________

^{(факультета, группы)}

_______________ ^{( ф.и.о.)}

Вариант 3

№ ____________ ^{(зачетная книжка)}

Москва-2014

Содержание

Введение………………………………………………………………………..3

Исходные данные……………………………………………………………..4

Задание 1………………………………………………………………………8

Задание 2………………………………………………………………………9

Задание 3………………………………………………………………………10

Задание 4………………………………………………………………………14

Задание 5………………………………………………………………………17

Список использованной литературы……………………………………….21

Введение

Цель курсовой работы - закрепить знания по дисциплине «Статистика»,  полученные в процессе изучения учебного материала; отработать навык практического решения задач статистике, причем как применения методики расчетов, так и составления выводов по полученным данным.

Все задания опираются на исходные данные выборочного наблюдения рабочих завода, состоящего из двух цехов.

Исходные данные

№ п/п	Разряд	Производственный стаж, лет	Заработная плата, у.е.
Цех № 1
1	4	5	539
2	1	1	487
3	4	7	554
4	2	2	507
5	1	1	490
6	2	5	519
7	3	8	536
8	5	10	574
9	2	0	481
10	3	7	533
11	2	2	515
12	2	3	524
13	5	5	553
14	1	1	479
15	3	4	509
16	3	8	552
17	2	3	526
18	2	1	495
19	1	0	492
20	4	6	562
21	2	5	516
22	1	0	483
23	4	8	531
24	4	12	548
25	2	4	521
26	3	7	529
27	3	6	520
28	2	1	475
29	3	8	525
30	1	0	472
31	4	3	553
32	2	4	518
33	1	0	485
34	2	3	508
35	3	8	507
36	5	17	578
37	2	1	505
38	6	23	600
39	3	4	528
40	3	11	538
Цех № 2
1	3	5	536
2	2	1	501
3	3	3	517
4	4	15	571
5	2	1	492
6	4	19	562
7	1	0	480
8	3	5	541
9	3	7	535
10	2	1	502
11	3	3	528
12	4	12	565
13	4	2	525
14	5	6	536
15	5	8	574
16	3	3	523
17	6	29	571
18	2	3	498
19	4	13	537
20	3	8	530
21	1	1	494
22	2	0	468
23	4	3	513
24	3	9	547
25	6	9	594
26	5	12	588
27	1	2	504
28	3	6	523
29	1	0	460
30	4	14	536
31	2	4	517
32	3	5	535
33	3	0	492
34	4	15	553
35	5	8	573
36	2	1	486
37	4	2	543
38	3	4	522
39	3	7	534
40	4	10	558
41	2	4	506
42	2	4	512
43	3	11	552
44	4	5	527
45	4	7	547
46	5	15	595
47	3	4	514
48	3	8	555
49	3	9	524
50	2	4	505
51	4	11	559
52	1	1	491
53	3	9	534
54	4	10	552
55	3	2	526
56	5	21	597
57	3	8	521
58	2	0	483
59	5	13	575
60	2	2	508

Задание 1.

Построить ряд распределения рабочих завода по общему стажу работы, выделив пять групп со следующими специализированными интервалами: 1) менее года; 2) от 1 до 2 лет; 3) от 3 до 5 лет; 4)от 6 до 10 лет; 5)от 11 лет и выше.

Группировка – это «расчленение» на группы и подгруппы по существенным признакам данных. В результате группировки единиц совокупности по какому-либо признаку – общий стаж работы. Статистические ряды распределения – упорядоченное распределение единиц совокупности на группы.

Общий стаж работы – количественный признак, выраженный конечными числами, значит, в данном варианте необходимо построить дискретный вариационный ряд распределения, в котором будут отражены  варианты (х – отдельные значения группировочного признака) и  частоты (f – числа, показывающие количество раз, которое этот признак встретится). Группировка по одному признаку, значит, необходимо построить групповую таблицу (простой ряд распределения).

Таблица 2 - Группировка рабочих по разряду по заводу.

Группировка рабочих по общему стажу (х)	Количество рабочих, чел. (f)	Сумма накопленных частот (S)
Менее 1 года	10	10
1-2 года	19	29
3-5 лет	27	56
6-10 лет	27	83
Свыше 11 лет	17	-
Итого:	100	-

Задание 2.

Определить моду и медиану стажа рабочих всего завода.

В статистике исчисляются мода и медиана, показатели, относящиеся к структурным средним. Их величина зависит от строения статистической совокупности. Модой называется значение признака (варианта), чаще всего встречающееся в изучаемой совокупности.

Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

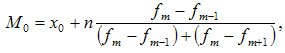
где:

-  — значение моды;

-  — нижняя граница модального интервала;

-  — величина интервала;

-  — частота модального интервала;

-  — частота интервала, предшествующего модальному;

-  — частота интервала, следующего за модальным.

Согласно исходным данным, сгруппированных в таблице 2, модальный интервал находится в пределах 3-5 и 6-10 лет, так как на этот интервал приходится наибольшая частота (27). Для определения медианного значения признака находят номер медианной единицы ряда (N_Me):

N_Me1=(3+5)/2=4;

N_Me2=(6+10)/2=8

Модальный интервал будет находиться в пределах 4-8 лет.

М₀=4+4*((27-19)/(27-19)+(27-17))=5,77 лет

Модальный стаж работы равен 5,77 лет.

Медианой в статистике называется варианта, расположенная в середине упорядоченного ряда данных, и которая делит статистическую совокупность на две равные части так, что у одной половины значения меньше медианы, а у другой половины – больше её. Для определения медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания или убывания индивидуальных значений признака.

Для установления медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половины суммы накопленных частот (в нашем случае 50)

Группировка рабочих по общему стажу (х)	Количество рабочих, чел. (f)	Сумма накопленных частот (S)
Менее 1 года	10	10
1-2 года	19	29
3-5 лет	27	56

 

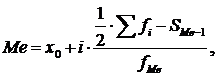
Где:

- x₀ – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); 

- i – величина медианного интервала; 

- S_Me-1 – накопленная интервала, предшествующего медианному; 

- f_Me – частота медианного интервала. 

Ме=3+2*0,5*(50-29)/27=3,3111

Данное значение показывает, что у одной половины рабочих стаж более 3,3 лет, а у другой менее 3,3 лет.

Задание 3.

Определить дисперсию производственного стажа рабочих в каждом цехе и по заводу в целом; среднюю из цеховых дисперсий; межцеховую дисперсию. Объяснить смысл дисперсий. Используя их, проверить правило сложения дисперсий.

Дисперсия представляет собой среднюю арифметическую из квадратов отклонений вариант от их средней арифметической и характеризует вариацию признака за счёт всех других признаков действующих внутри совокупности.

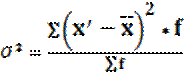
Таблица 3 – Распределение рабочих цеха №1 по стажу

Стаж		f	x'*f
До 1	5	0,5	2,50	4,51	22,56	101,81
1-2	8	1,5	12,00	3,51	28,10	98,70
3-5	12	4	48,00	1,01	12,15	12,30
6-10	11	8	88,00	2,99	32,86	98,18
Свыше 10	4	12,5	50,00	7,49	29,95	224,25
Итого	40		200,5		125,63	535,24

Таблица 4 – Распределение рабочих цеха №2 по стажу

Стаж		f	x'*f
До 1	5	0,50	2,50	5,66	28,29	160,08
1-2	11	1,50	16,50	4,66	51,24	238,70
3-5	15	4,00	60,00	2,16	32,38	69,88
6-10	16	8,00	128,00	1,84	29,47	54,27
Свыше 10	13	12,50	162,50	6,34	82,44	522,82
Итого	60		369,50		223,82	1045,75

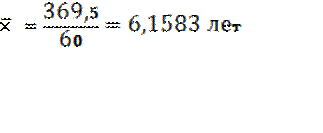
Таблица 5 – Распределение рабочих завода по стажу

Стаж		f	x'*f
До 1	10	0,50	5,00	5,20	5,20	52,00
1-2	19	1,50	28,50	4,20	4,20	79,80
3-5	27	4,00	108,00	1,70	1,70	45,90
6-10	27	8,00	216,00	2,30	2,30	62,10
Свыше 10	17	12,50	212,50	6,80	6,80	115,60
Итого	100		570,00		355,40	1612,50

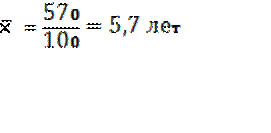
Общая дисперсия ) представляет собой среднюю арифметическую из квадратов отклонений вариант от их средней арифметической. Она характеризует вариацию признака за счёт всех других признаков действующих внутри совокупности. Дисперсия (взвешенная) определяется следующим образом:

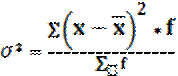
Групповая дисперсия (  )отражает вариацию признака за счет условий и причин, действующих внутри группы.

Средняя из групповых дисперсий() считается (данная формула используется