Расчет основных характеристик цифровой системы передачи непрерывных сообщений, страница 4

Записываю аналитическое выражение, связывающее сигналы z(t) и u(t) с учетом аддитивного шума и коэффициента K_nk

 

 

 

Нахожу мощность шума на выходе канала P_ш в полосе частот модулированного сигнала F_u.

                                                                                                                                                                                                               

Нахожу мощность P_s модулированного сигнала s(t)=K_nku(t) на входе демодулятора.

                       

Определяю отношение сигнала к шуму на выходе канала P_s / P_ш в децибелах.

P_s / P_ш= 1,04

Определяю энергию элементарного символа принятого полезного сигнала длительностью Т

 

Рассчитываю значение параметра h² – отношение энергии сигнала к СПМ шума на входе демодулятора.

!  

Определяю пропускную способность канала С’.

С=ΔF_u·log₂(1+P_с/P_ш)=286·10³·log₂(1+1,04)=286·10³_·1,43=408,98 кбит/с

Рассчитываю эффективность использования пропускной способности канала К_с, определяемую как отношение производительности источника сообщений Н’(В) к пропускной способности непрерывного канала  С’.

                                         К_с=Н(В)/С=90·10³/408,98·10³=0,22

7. ДЕМОДУЛЯТОР

Структурная схема оптимального демодулятора для заданного вида модуляции и способа приема. Способ сравнения фаз (некогерентный прием).

Полосовой фильтр отсекает помехи вне полосы сигнала. Элемент памяти задерживает сигнал на один единичный интервал. ФД - сравнивает сигнал с предыдущим - задержанным. Если фазы совпадают, то принята "1", если нет то "0".

Рассчитываю среднюю вероятность ошибочного приема двоичного символа р_ош

8. ДЕКОДЕР

Оцениваю обнаруживающую способность q₀ заданного кода (n, n-1) c одной проверкой на четность.

d_min=2;    q₀=d_min-1=1

Рассчитываю вероятность необнаруженной ошибки р_но.

Код с одним битом проверки на четность обнаруживает одиночные ошибки. В соответствии с формулой (7.3) курса лекций и с учетом всего 8 символов в комбинации, вероятность того, что ошибок в кодовой комбинации будет больше, чем в одном символе

,     где  p=p_{ош ОФМ},                   

Из этих слагаемых выбираю только те, которые соответствует четному числу ошибок, т.к. остальные обнаруживаются. Это и будет искомая вероятность не обнаруживаемой ошибки:

Очевидно, что р_(i=4) ≈ 0, р_{(i=6 )} ≈ 0,  тогда    р_но ≈ р₂+р₄=0,001621+2,498*10^-7=0,001621516    

9. ФИЛЬТР НИЖНИХ ЧАСТОТ

Определяю значение F_ср ФНЧ, при котором обеспечивается теоретически точное восстановление непрерывного сообщения.

Непрерывный сигнал может быть восстановлен по своим отсчетам с помощью идеального ФНЧ, частота среза которого F_ср определяется выбранным интервалом дискретизации Δt в соответствии с теоремой Котельникова.

Амплитудно-частотная характеристика ФНЧ

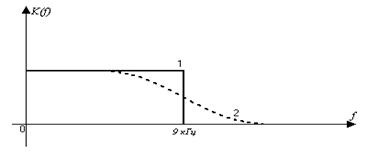                  1 – идеальный фильтр

2 – реальный фильтр

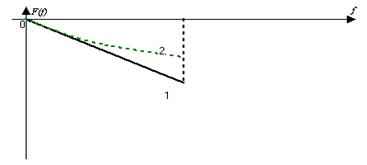
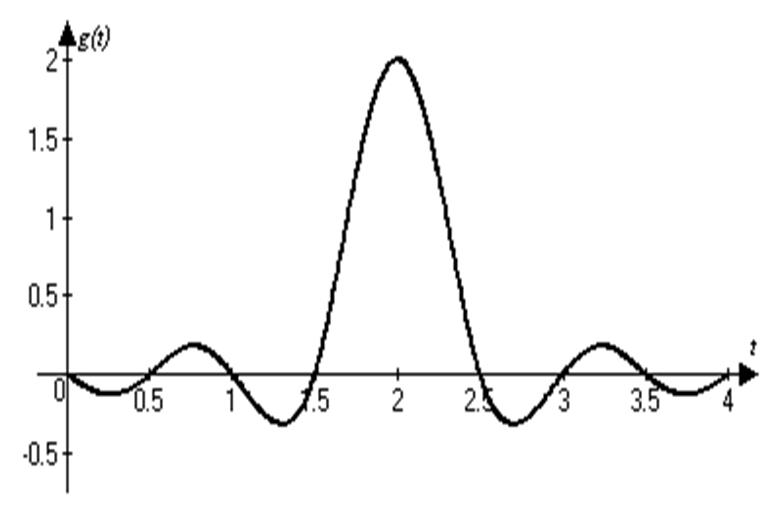
Нахожу импульсную характеристику g(t) ФНЧ и строю график.

Импульсная реакция фильтра связана преобразованием Фурье с комплексным коэффициентом передачи:         

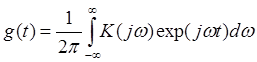
K(jω) примем равным 1 при -2πF_ср<ω<2πF_ср  и  K(jω)=0 вне этого интервала.

На оси времени введем также параметр τ – время задержки максимума импульсной характеристики относительно начала импульсного воздействия на ФНЧ. Это время зависит от крутизны фазочастотной характеристики, которая на практике тем выше, чем ближе реальный фильтр к идеальному, иначе говоря, чем выше порядок фильтра. Тогда:

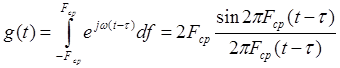
Для упрощения расчетов и построений произведем нормирование импульсной характеристики относительно частоты среза фильтра F_ср = 9000 Гц: