Расчет основных характеристик цифровой системы передачи непрерывных сообщений, страница 3

Записываю комбинацию примитивного двоичного кода, соответствующего передаче j-го уровня, считая, что она представляет собой запись числа j в двоичной системе счисления.

j=77 в двоичном виде:   1001101     

                                             b₇b₆       b₅      b₄     b₃      b₂      b₁

Алгоритм:  1*2⁶+1*2⁵+1*2⁴+1*2³+1*2²+1*2¹+1*2⁰

7        6        5        4       3        2        1    (разряды)

Кодовая комбинация примитивного кода:  1001101

Записываю соответствующую комбинацию кода с проверкой на четность, указав в ней информационные и проверочный разряды.

Проверочный разряд b₈=b₇+b₆+b₅+b₄+b₃+b₂+b₁=0

В результате получаем кодовую комбинацию кода с проверкой на четность: 01001101 (проверочный символ – слева).

Определяю число двоичных символов, выдаваемых кодером в секунду (скорость манипуляции) V_k и длительность передачи символа (тактовый интервал синхронного двоичного сигнала) Т.

5. МОДУЛЯТОР

Записываю аналитическое выражение модулированного сигнала u(t), связывающее его с сигналом b_икм(t).

На выходе модулятора при ФМ при каждой передаче посылки «1» производится смена фазы несущей на 180^о, а при передачи символа «0» фаза не изменяется.

u(t)=cos2πƒt при 0<t<∆t   

u(t)=-cos2πƒt при ∆t <t<4t

u(t)=cos2πƒt при 4t<t<7t

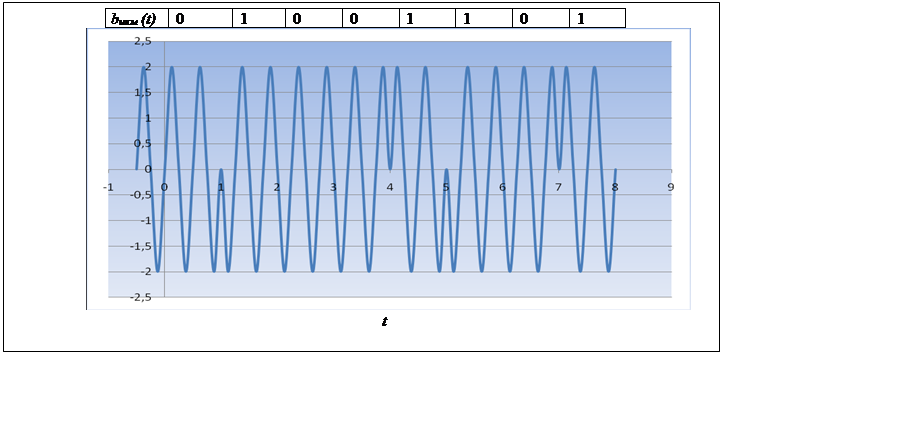
Строю графики временных диаграмм сигналом b_икм(t) и соответствующего модулированного сигнала u(t) (с учетом заданного вида модуляции).

u(t)

 

Записываю аналитическое выражение и построю график автокорреляционной функции R_икм(τ) для последовательных кодовых символов b_икм(t), поступающих на вход модулятора. Вычисление и построение провожу применительно к одиночному символу длительностью Т, что соответствует минимально возможному интервалу автокорреляции и максимальной ширине энергетического спектра.

Общая формула для корреляционной функции:

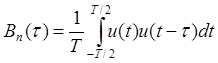
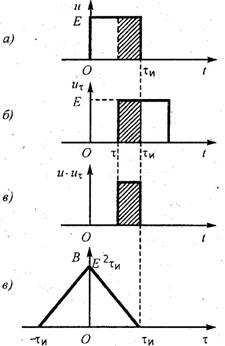  Для получения аналитического выражения корреляционной функции первичного (модулирующего) сигнала используем прием графического вывода формулы КФ случайного синхронного двоичного (телеграфного) сигнала (см. рисунок слева). Из рисунка следует, что B(τ)=E²·(τ_u-|τ|) при временном сдвиге  |τ|<τ_u. Следовательно, после нормирования корреляционной функцииB(τ) относительно максимумаE² получим искомые выражение и график:

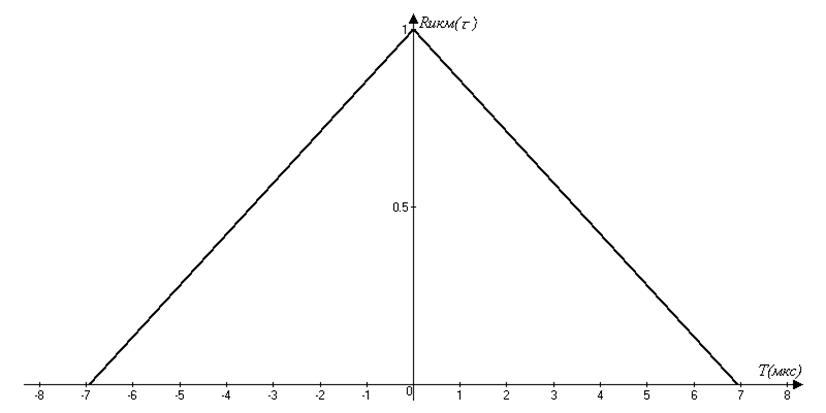
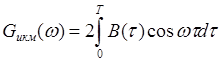Записываю аналитическое выражение и строю график СПМ (спектральной плотности мощности, энергетического спектра) G_икм(f) этого сигнала.

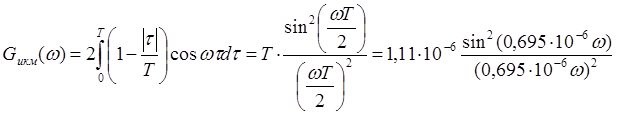
Значение ω_k, при кратности которым имеют место нулевые значенияG_икм(ω):

   

,           где k=±1;±2…±n           

Произвожу вычисления СПМ (спектральной плотности мощности, энергетического спектра) G_икм(f) этого сигнала.

ω	Gикм(ω)[Вт/Гц]	f= ω/2π
0	1,11·10-6	0
0,225·106	1,11∙10-6	0,036·106
0,45·106	1,076∙10-6	0,072·106
0,9·106	0	0,143·106
1,35·106	0,973∙10-6	0,215·106
1,8·106	0	0,286·106
2,25·106	0,454∙10-6	0,359·106
2,7·106	0	0,43·106

Записываю аналитическое выражение и строю график энергетического спектра модулированного сигналаG_u(f)  для единичного импульса.

  

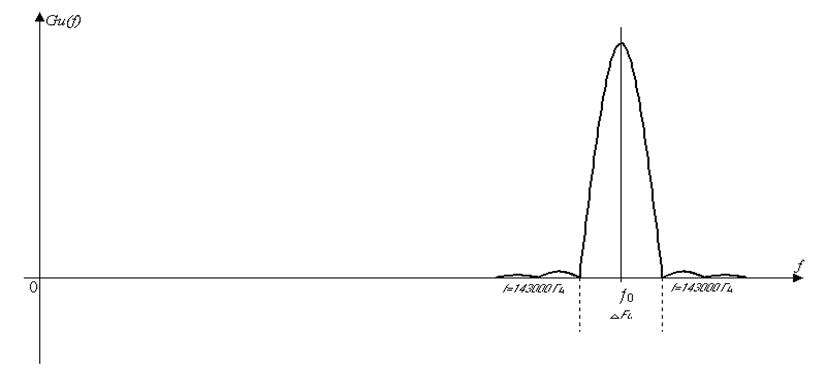
Вычисляю полосу частот (ширину энергетического спектра) модулированного сигнала

6. КАНАЛ СВЯЗИ