Расчет основных характеристик цифровой системы передачи непрерывных сообщений, страница 2

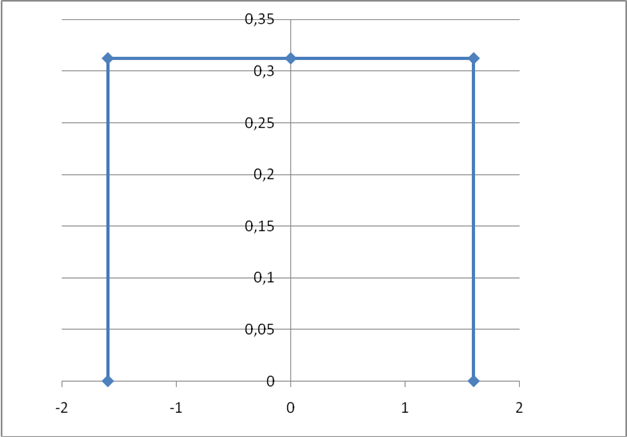
Источник сообщений выдает сообщение b(t), представляющее собой непрерывный стационарный случайный процесс, мгновенные значения которого в интервале от -1,6 до +1,6 В.

Сигналы в системах передачи информации и действующие в них помехи по своей природе являются случайными процессами. Для их описания необходимо применять математический аппарат теории вероятностей и случайных процессов.

Плотность распределения вероятностей.

Одномерная плотность распределения вероятностей p(x,t) случайного процесса Х(t) (плотность вероятностей - ПВ) характеризует распределение вероятностей реализации случайной величины Х(ti) в произвольный момент времени ti. Она представляет собой производную от функции распределения вероятностей: 

p(x,t_i) dx =1 

Для данного случая;

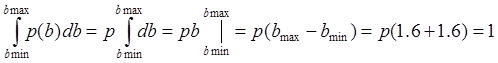
P(b)=0  при b<-1,6; b>1,6

P(b)=1/3,2=0,3125  при b>-1,6; b<1,6

Интегральная функция распределения.      

Интегральная функция распределения (ИФР)  F(x,ti)   определяет вероятность того, что в момент времени ti значение случайной величины X(ti) не превысит значения x:

F(x,ti) = P[X(ti)≤x].

Функция F(x,t) является неубывающей с предельными значениями F(-∞,t)=0 и F(∞,t)=1. При известной функции F(x,t) вероятность того, что значение X(ti) в выборках будет попадать в определенный интервал значений [a, b] будет определяться выражением:

P[a<X(ti)≤b] = F(b,ti) – F(a,ti).

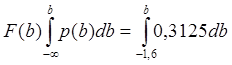
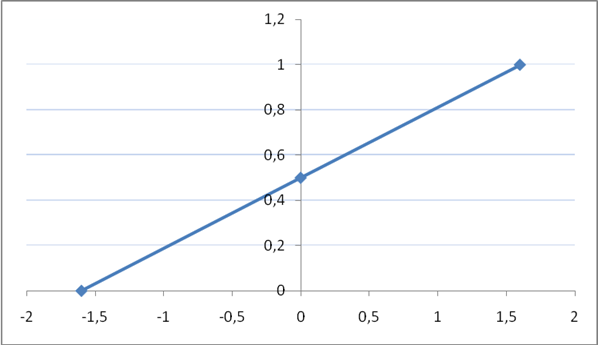
F(b)=0   при b<-1,6

F(b)=(b+1,6)/3,2  при b>-1,6; b<1,6

F(b)=1 при b>1,6

Математическое ожидание.

Математическое ожидание (МО) представляет собой статистическое усреднение случайной величины X(t_i),

m_x(t) º M[Х(t] = x p(x;t) dx,

Математическое ожидание m_x(t) представляет собой неслучайную составляющую случайного процесса X(t). 

Для данного случая;

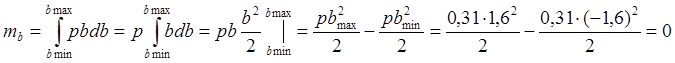
Дисперсия.

Функция дисперсии D_x(t) случайного процесса является теоретической оценкой среднего взвешенного значения разности [Х(t)-m_x(t)]²:

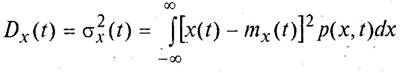
Дисперсия характеризует разброс мгновенных значений реализаций случайного процесса относительно его среднего значения.

Физический смысл величины среднеквадратического отклонения (СКО) _x(t) - действующее значение случайного напряжения или тока на единичном сопротивлении, a D_x(t)- мощность переменной составляющей случайного процесса.

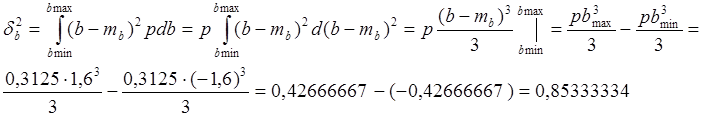Для данного случая;

3. ДИСКРЕТИЗАТОР И КВАНТОВАТЕЛЬ

Согласно теоремы Котельникова допустимый интервал дискретизации первичного сигнала b(t) по времени

Число уровней квантования

                                                                                                                     

Средняя мощность шума квантования

Рассматривая дискретизатор и квантователь вместе, как источник дискретных  сигналов B={b_кв(t_i)} с объемом алфавита L, определяем его энтропию Н(В) и производительность Н’(В) при условии, что отсчеты, взятые через интервал ∆t, статистически независимы.

4. КОДЕР

Определяю число информационных символов двоичного кода k, необходимое для кодирования всех Lуровней квантованного сообщения.

                                                                                

Определяю длину кодовой комбинации n кода с одной проверкой на четность.                                                                                                                                             

Нахожу избыточность кода ρ.