Побудова системи черезшкірного живлення електрокардіостимулятора, страница 3

Корпус імплантанта виготовляють з легкого, корозостійкого, міцного металу – титану (Ti). Електропровідність титану  См/м.

Оскільки сучасні кардіостимулятори характерні невеликим споживанням електроенергії, буде достатньо електроємності акумулятора 0.5 А∙год. для отримання періодичності заряджання в 1÷2 роки. Заряджання акумулятора повинно відбуватись швидко, щоб завдати організму пацієнта мінімально можливих ушкоджень, а також зменшити час процедури. Тому заряджання повинно проводити максимально допустимим струмом, який для літій-іонних акумуляторів становить1 C (C – ємність елемента) [3].

Оскільки передача енергії повинна відбуватися з допомогою магнітного поля, бо електричні поля впливатимуть на функціонування серця, за незалежну змінну, через яку будуть визначатись всі розрахункові параметри, візьмемо векторний магнітний потенціал. Джерелом електромагнітного поля виберемо котушку індуктивності. Приймачем – також котушку індуктивності співвісну до першої. При використанні такої співвісної системи котушок, тривимірну задачу можна звести до плоскої осесиметричної задачі. При цьому напрямки векторів густини струму J, магнітного потенціалу А, і електричного поля Е будуть перпендикулярні площині січення області рішення задачі, тому їх можна розглядати як скалярні величини. Вектори магнітного поля Н і магнітної індукції В будуть лежати в площині січення області рішення задачі. Для гармонічного сигналу операція диференціювання еквівалентна множенню на , де .

2.1.2.  Математична модель. Основними рівняннями, розв’язком з яких випливає рівняння електромагнітної хвилі є рівняння Максвела:

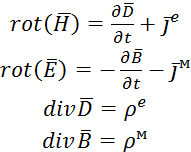,                                          (1)

де  і  ‑ вектори напруженості електричного і магнітного полів;  і  ‑ вектори електричної і магнітної індукції;  і  ‑ вектори об’ємної густини електричного і магнітного струму;  і  ‑ об’ємні густини електричного і магнітного зарядів. Властивості середовища враховуються матеріальними рівняннями:

                                                    (2)

Рівняння (1) за лінійності рівнянь (2) є системою лінійних рівнянь в частинних похідних першого порядку.

Рівняння хвилі з рівнянь (1) отримаємо шляхом застосування векторного і скалярного потенціалів, вважаючи середовище однорідним та ізотропним. В рівняннях (1) поле представлено у вигляді суперпозиції поля від електричних струмів  і поля від магнітних струмів , де індекси «» та «» позначають поля від сторонніх електричних та магнітних струмів. Тоді, для електричних струмів векторний потенціал  і скалярний потенціал  вводиться з допомогою рівностей:

.                        (3)

Для магнітних струмів ‑ потенціали  і :

.                   (4)

Враховуючи (3,4) рівняння (1) набирають вигляду:

де  ‒ густина зовнішніх джерел струму. Таке представлення зручне тим, що проміжними результатами будуть величини магнітних і електричних полів, що зручно для спрощення розрахунків. В якості джерела магнітного поля при цьому зручно задавати величину густини струму в області поперечного перерізу випромінюючої котушки.

Рівняння для миттєвих значень векторних скалярних потенціалів наберуть вигляду:

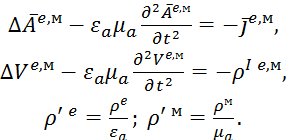                              (6)

тут  оператор Лапласа.

З урахуванням припущень, наведених в (2.1.1) основне рівняння (5) набирає вигляду [4].

                         (7)

де  ‒ абсолютна діелектрична проникність вакууму ,  ‒ абсолютна магнітна проникність вакууму   і  ‒ відносні (relative) величини діелектричної проникності відповідно.