














Зміст:
1. Вступ.
2. Постановка задачі.
3. Вихідні дані.
4. Алгоритм RADAUS.
5. Розв’язок методом алгоритму RADAUS.
6. Алгоритм Булирша-Штерна.
7. Розв’язок методом Булирша-Штерна.
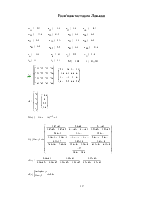
8. Реалізація перетворення Лапласа засобами MathCAD.
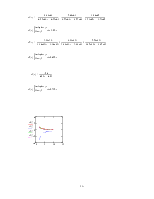
9. Розв’язок методом Лапласа.
10. Метод Рунге-Кутта.
11. Розв’язок методом Рунге-Кутта з фіксованим кроком.
12. Розв’язок методом Рунге-Кутта зі змінним кроком.
13. Висновки.
Вступ
Бурхливий розвиток в останнє десятиліття інформаційних технологій і комп'ютерної техніки сприяє виникненню усе більше складніших математичних задач, для рішення яких без застосування чисельних методів потрібний значний проміжок часу.
Однією з таких задач є рішення систем диференціальних рівнянь. Ряд фізичних задач може бути зведений до рішення диференціальних рівнянь або системи диференціальних рівнянь. Задача рішення системи диференціальних рівнянь має важливе прикладне значення при рішенні наукових і технічних проблем. Крім того, вона є допоміжною задачею при реалізації багатьох алгоритмів обчислювальної математики, математичної фізики, обробки результатів експериментальних досліджень. Нажаль, лише дуже малу частину таких задач можливо вирішити без допомоги обчислювальних машин. Тому для інженерів надто важливо вміти знаходити рішення диференціальних рівнянь за допомогою програмного забезпечення. Даний курсовий проект включає в себе розв’язок системи диференціальних рівнянь за допомогою програми MathCAD 14.
Постановка задачі
¾ Розв'язати систему диференціальних рівнянь, задану в формі Коші;
¾ Визначити аналітичні залежності змін стану системи при заданих початкових умовах і відсутності зовнішнього впливу з використанням функції MathCAD;
¾ Знайти частинний розв'язок неоднорідної системи диференціальних рівнянь;
¾ Розв'язати із застосуванням функцій MathCAD;
¾ Знайти частинний розв'язок неоднорідної системи диференціальних рівнянь;
¾ Знайти розв'язок неоднорідної системи диференціальних рівнянь при заданому зовнішньому впливі та початкових умовах за допомогою функції MathCAD;
¾ Зробити висновки.
Вихідні дані:
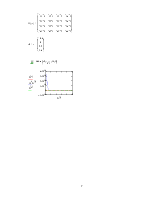
Електротехнічна система описується заданою системою лінійних диференціальних рівнянь з 4 шуканими функціями
х0(t), x1(t), x2(t), x3(t)
Система лінійних диференціальних рівнянь у формі Коші
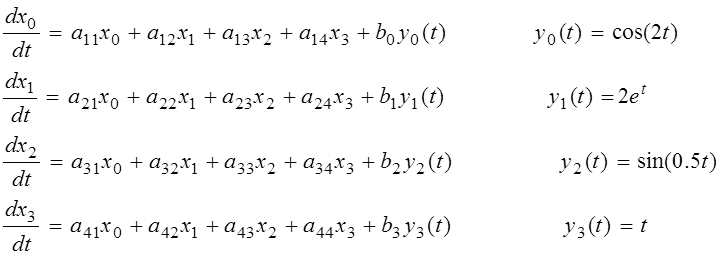
|
№ варіанту |
Коефіцієнти системи диференціальних рівнянь |
Початкові умови |
||||||||||||||||||
|
а11 |
а12 |
а13 |
а14 |
а21 |
а22 |
а23 |
а24 |
а31 |
а32 |
а33 |
а34 |
а41 |
а42 |
а43 |
а44 |
х0(0) |
х1(0) |
х2(0) |
х3(0) |
|
|
3 |
2,3 |
-1,6 |
1,4 |
-1,3 |
-3,6 |
8,3 |
6,6 |
6,4 |
3,4 |
4,3 |
-1,0 |
6,4 |
6,4 |
2,2 |
6,6 |
-2,8 |
-0,8 |
0 |
2,2 |
1,6 |
Алгоритм RADAUS
Вирішення жорстких систем диференціальних рівнянь можна здійснити за допомогою вбудованої функції: Radau(y0,t0,t1,m,f) — алгоритм RADAUS для жорстких систем ЗДУ, де у0 — вектор початкових значень в точці to; t0, t1 — початкова і кінцева точки розрахунку; m — число кроків чисельного методу; f — векторна функція F(t, у) розміру 1xn, що задає систему ЗДУ;
Рішення видається у вигляді матриці, за формою ідентичною аналогічним функціям вирішення нежорстких задач Коші.
Вбудована функція Radau, яка не вимагає явного завдання якобіана системи рівнянь, з'явилася у версії MathCAD 2011.
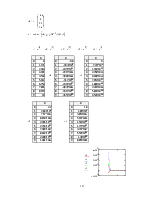
Розв’язок методом алгоритму RADAUS
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгоритм Булирша-Штерна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.