Локализация корней нелинейных уравнений. Вычисление корней нелинейных уравнений с заданной точностью

Чувашский Государственный Университет имени И. Н. Ульянова

Кафедра высшей математики

Курсовая работа по теме:

ЛОКАЛИЗАЦИЯ КОРНЕЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

ВЫЧИСЛЕНИЕ КОРНЕЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ С ЗАДАННОЙ ТОЧНОСТЬЮ.

   Выполнил: студент

   группы ИВТ-41-12

   Принял:

   Доц.

Чебоксары 2012 г.

СодержаниЕ

1. Введение----------------------------------------------------------------------------------------2.1 лОКАЛИЗАЦИЯ КОРНЕЙ-----------------------------------------------------------------2.2 уТОЧНЕНИЕ КОРНЕЙ----------------------------------------------------------------------3. Методы уточнения корней--------------------------------------------------------3.1 Метод половинного деления (бисекции, дихотомии)--------3.2 Метод хорд-----------------------------------------------------------------------------------3.3 Метод Ньютона (метод касательных)-----------------------------------3.4 Модифицированный метод Ньютона------------------------------------

3.5. Метод простых иттераций------------------------------------------------------

4.вЫВОДы-------------------------------------------------------------------------------------------

5.Приложения----------------------------------------------------------------------------------

6. иСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА-----------------------------------------------------

1.Введение

Задача отыскания корней нелинейных уравнений вида

f(x)=0 (1.1)

встречается в различных областях научных исследований.

Все нелинейные уравнения можно разделить на два типа:

— алгебраические;

— трансцендентные.

Алгебраическими называются уравнения, содержащие только алгебраические функции (например, полином). Уравнения, содержащие функции (тригонометрические, логарифмические и др.) называются трансцендентными.

Как правило, встречающиеся на практике уравнения не удается решить точными методами, когда решение уравнения можно записать в виде конечной формулы. Так методы решения линейных и квадратных уравнений были известны ещё древним грекам. Решение алгебраических уравнений третьей и четвертой степеней было получено итальянскими математиками Ферро, Кардано, Феррари в XV веке. Однако, как доказал в 20-ых годах XIX века норвежский математик Н.Абель, общее уравнение пятой и более высоких степеней неразрешимо в радикалах.

Для трансцендентных уравнений задача поиска корней ещё более осложняется.

Возьмем в качестве модельного очень простое уравнение

f(x)=x-cosx=0 (1.2)

Это уравнение имеет единственный корень (x≈0.73), однако получить формулу для его вычисления невозможно.

В тех случаях, когда не удается найти аналитическое решение уравнения, важное значение приобретают универсальные вычислительные методы отыскания корней. Обычно эти методы не накладывают ограничений на конкретный вид функции f(x), а предполагают только, что она обладает некоторыми свойствами типа непрерывности, дифференцируемости и т.д. Такие методы называют, как правило, итерационными, т.е. позволяющие получать лишь приближенное значение корня за некоторое число шагов.

Большинство этих методов предполагают, что заранее известны достаточно малые окрестности, в каждой из которых имеется только один корень.

Таким образом, задача приближенного вычисления корней уравнения       f(x) =0 распадается на две задачи:

— отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых  заключен только один корень уравнения;

— нахождение корня с достаточной точностью, если известно некоторое начальное его приближение.

Приближенное значение корня может быть найдено различными способами: из физических соображений, из решения аналогичной задачи при других исходных данных, с помощью других графических методов.

Уточняющие методы позволяют отыскать действительный корень уравнения f(x) = 0, как правило, с контролируемой точностью. Отметим, что уточняющие методы описываются для решения трансцендентных уравнений, однако все нижеописанные способы решения трансцендентных уравнений могут использоваться для отыскания действительных корней алгебраических уравнений.

2.1.  Локализация корней.

Для отделения корней уравнения (1.2) необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке  имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция  непрерывна на отрезке ,  а на концах отрезка её значения имеют разные знаки , то на этом отрезке расположен, по крайней мере, один корень. Это условие (как видно из рисунка 2.1) не обеспечивает единственности корня. Достаточным дополнительным условием, обеспечивающем единственность корня на отрезке  является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства первой производной .

Таким образом, если на отрезке  функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень. Заметим, что под этот критерий не подпадают кратные корни уравнений, например, очевидный корень уравнения .

Воспользовавшись этим критерием можно отделить корни аналитическим способом, находя интервалы монотонности функции.

Отделение корней можно выполнить графически, если удается построить график функции . В ряде случае бывает удобно заменить уравнение  эквивалентным уравнением вида . Корни этого уравнения 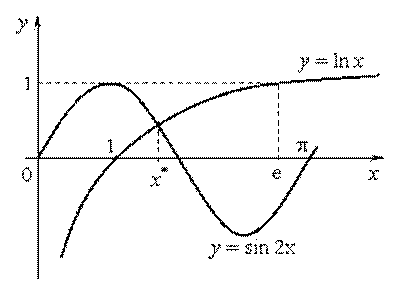определяются абсциссами точек пересечения графиков функций  и .

(рис2.2) Табличный способ локализации корней уравнения   (рис.2.3)Графическое отделение корней sin 2x-lnx

В качестве примера рассмотрим уравнение .Переходя к эквивалентному уравнению  построим графики функций  и  (рис. 2.3)

Из графика видно, что уравнение содержит один корень, расположенный