Методы математической статистики и теории вероятностей в выборе фильма, страница 6

Меры изменчивости говорят о том, в какой степени полученные результаты отклоняются от «центра группирования», что чаще всего приводит к определению меры отклонения экспериментальных данных от среднего. В принципе, в качестве меры изменчивости можно было бы использовать среднее значение отклонений текущих значений от среднего. Для этого необходимо определить, насколько каждое значение количества фильмов отклоняется в большую или меньшую сторону от X—2,895 затем сложить все результаты и разделить на число значений. К сожалению, этот путь невозможен, поскольку, как правило, отклонения от среднего в большую сторону (со знаком «+») и в меньшую сторону (со знаком «—») компенсируют друг друга и в сумме дают ноль. Для решения этой проблемы лучше использовать не отклонение от среднего, а квадрат этого отклонения, потому что такая процедура позволяет избавиться от влияния знака. Вначале делается та же операция — определяется, насколько каждое значение возраста отклоняется в большую или меньшую сторону от Х= 2,85. Затем каждый из полученных результатов возводится в квадрат, все складывается и делится на число значений. Получаемая таким образом мера изменчивости называется дисперсией. Данные приведены в таблице 1.7.

Таблица 1.7

Вычисление дисперсии

Число фильмов	Частота	(Число фильмов-Среднее)	(Число фильмов - Среднее)2	(Частота)*(фильмов - Среднее)2
1	10	-1,85	3,42	34,2
2	25	-0,85	0,72	18
3	40	0,15	0,02	0,8
4	20	1,15	1,32	26,4
5	5	2,15	4,62	23,1

.

Подставим в эту формулу необходимые значения из таблицы

К сожалению, дисперсия оказывается не очень удобным показателем меры изменчивости.

Для решения возникшей проблемы вместо значения дисперсии используется квадратный корень из нее. Полученное таким образом новое значение называется стандартным отклонением и является наиболее популярной мерой изменчивости. Стандартное отклонение часто обозначается как  (сигма):

Для нашего случая:

.

Проверим гипотезу по формуле Стьюдента .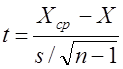

Выбирается уровень значимости a и критическая область А, так, чтобы условная вероятность попадания критерия в А при условии справедливости гипотезы  равнялась a.

Выберем a=0.05 (вероятность не принять верный прогноз). По табл. распределения Стьюдента находим критическое значение (квантиль) (см. Приложение Таблица2)  

критерия

Þ  Р{|t|>1,725}=0.05,

Þ  критическая область А:

|t|>1,725.

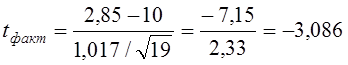
То есть прогноз должен быть отвергнут, так как отклонение от него в сторону повышения не является случайностью.

Гипотеза о том, что прогноз верен, проверена по критерию 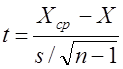 на уровне значимости 5% и отвергнута.

2 СРАВНЕНИЕ РАЗМАХА КОЛИЧЕСТВА ПРОСМОТРЕННЫХ ФИЛЬМОВ ОТЕЧЕСТВЕННОГО И ЗАРУБЕЖНОГО ПРОИЗВОДСТВА

2.1 Жанры киноиндустрии.

В современном мире киноиндустрии существует множество жанров, согласно которым классифицируют все фильмы. Фильмы распределяют в зависимости, от эмоций, которые хотел вызвать у зрителей режиссёр данной картины.

Артхаус— фильм, нацеленный не на массовую аудиторию. Подобные фильмы прежде всего некоммерческие, самостоятельно сделанные фильмы, а также фильмы, снятые маленькими киностудиями или, так называемые, короткометражные фильмы. Биография -  жанр кинематографа, повествующий о судьбе знаменитой или известной личности. Фильм-биография пытается всесторонне передать жизнеописание личности или хотя бы годы, сыгравшие наиболее важную роль в жизни человека.

Боевик - жанр кинематографа, в котором основное внимание уделяется насилию: перестрелкам, дракам, погоням и т. п.  Такие фильмы часто обладают высоким бюджетом, изобилуют каскадёрскими трюками и спецэффектами.

Военный - исторический художественный фильм, реконструирующий события реально происходившей войны или сражения, приёмы и организацию боя. В центре художественной композиции такого фильма обычно находится сцена главного сражения, съёмки которого сочетают широкие панорамные планы с крупными планами героев фильма.