Методы математической статистики и теории вероятностей в выборе фильма, страница 5

Новая таблица содержит ту же самую информацию, что и предыдущая, но она заметно короче, данные в ней упорядочены по возрастанию, и с ней удобней работать.

Медиана () представляет собой значение, которое делит упорядоченные данные пополам таким образом, что одна половина данных оказывается меньше медианы, а другая — больше.

Нахождение медианы не носит столь наглядного характера, как нахождение моды. Для определения медианы приходится прибегать к дополнительным преобразованиям и вычислениям. Во-первых, дополним таблицу еще двумя строками и получим таблицу 1.6.

Таблица 1.6

Частота, накопленная частота и процент встречаемости фильмов

В первой из дополнительных строк запишем значения так называемых «накопленных» (или кумулятивных) частот, которое будет равно 100.

Во-вторых, запишем в следующую графу, какой процент от 100

составляет каждое значение накопленных частот. В нашем случае значения третей и четвертой строк совпадают, так как частота равняется 100. Вообще могут получаться не одинаковые значения.

Попытаемся понять смысл полученного в последней графе результата.

При переходе от столбца со значением числа фильмов «2» к столбцу со значением  «3» за плечами остается 35% всех результатов. А при переходе от столбца со значением «3» к столбцу «4» за плечами уже 75%. Медиана — это та точка, которая делит все данные в  отношении 50:50. Очевидно, требуемая точка где-то внутри столбца со значением «3». То есть

Для нахождения среднего используется простая формула, смысл которой в том, чтобы сложить все значения(в нашем случае значения количества встреченных «отечественных» фильмов) и разделить полученный результат на число значений (в нашем случае 100).

Дальше можно идти двумя путями.

Во-первых, начать непосредственно складывать все 100 значений из первой таблицы.

Во-вторых, догадаться, что если некоторые значения количества просмотренных фильмов встречаются несколько раз, то можно воспользоваться данными из таблицы 1.2 и перейти от сложения повторяющихся значений к умножению этих значений на число повторов(например, число машин 1 встречается в первой таблице 10 раз, значит вместо 1 + 1 + 1 + 1+1+1+1+1+1 можно записать  1x10). Тогда:

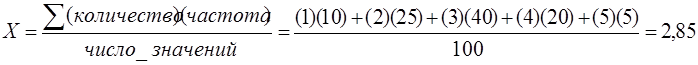
Среднее значение получилось близким к трем.

Исходя их найденных значений моды, медианы и среднего, можно утверждать, что данное распределение можно считать нормальным, так как значения моды и медианы абсолютно равны, а значение среднего отличается на 0,15. Если взять большее количество испытаний, то среднее значение будет приближаться к трем. 

На диаграмме 1, можно просмотреть, что закон распределения стремится к нормальному.

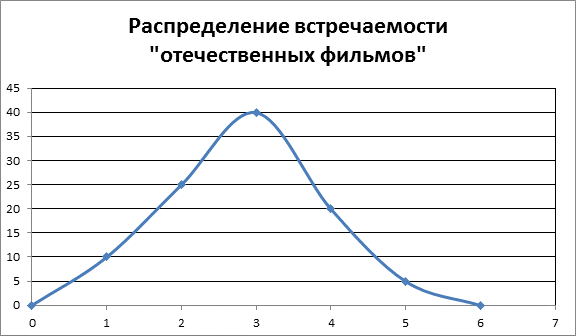
Диаграмма 1.

Теперь приступим к проверке гипотезы.

Н0: Вероятность встретить на сайте megogo.net фильм отечественного производства, равна вероятности встретить фильм, произведенный в зарубежных странах.

Н1: Вероятность встретить на сайте megogo.net фильм отечественного производства, не равна вероятности встретить фильм, произведенный в зарубежных странах.

Наш прогноз , выборка , средняя .

Меры центральной тенденции показывают, вокруг каких значений  группируется большинство экспериментальных данных. Обычно в качестве «центра» такого группирования рассматривается среднее (X).