Методы наложения для определения токов ветвей.Частные токи для схемы у которой имеется один источник, страница 3

Определим токи ,   схемы рисунок 1.3.

Определим действительные токи цепи рисунок1.2 как алгебраическая сумма    

частных токов.

Таким образом, полученные значения токов ветвей по методу наложения      совпадают со значениями данных токов, рассчитанных по методу   контурных         токов , следовательно токи ветвей схемы рисунок1.1 определены правильно.

Так как  Рист = Рпр, то баланс мощностей выполняется. Следовательно, токи в      ветвях схемы определены правильно.

Как видно расчет токов ветвей обоими методами показал, что значение токов  одинаково и следовательно токи рассчитаны правильно.

Вт

Вт

6. Определим значение тока    методом эквивалентного генератора. Для этого     разорвем цепь так, как это показа на рисунке1.4  

(R1+ r01 +  R3 ) Ik1  -  R3  Ik2  =   E1

- R3  Ik1  +  (R3 + R4 + R5)  Ik2  =  0

Определим  напряжение холостого  Uxx на разомкнутом участке цепи (рис.1.4) :

=

Определим эквивалентное сопротивление цепи по отношению к зажимам Uxx. При этом данное сопротивление Rэквхх  равно рассчитанному выше Rэкв2 в пункте 3.2.  

Отсюда значение тока  равно: 

=

Рисунок1.4-Схема контурных токов

Определим токи в ветвях схемы рисунка 1.4. Обозначим на схеме контурные             токи Ik1 и Ik2 и составим систему уравнений по методу контурных токов.

Подставим в систему числовые значения и решим ее методом определителей: 

Ом

А 

Полученное значение тока  равно значению тока , рассчитанного ранее по       методу контурных токов и методу наложению, что подтверждает правильность

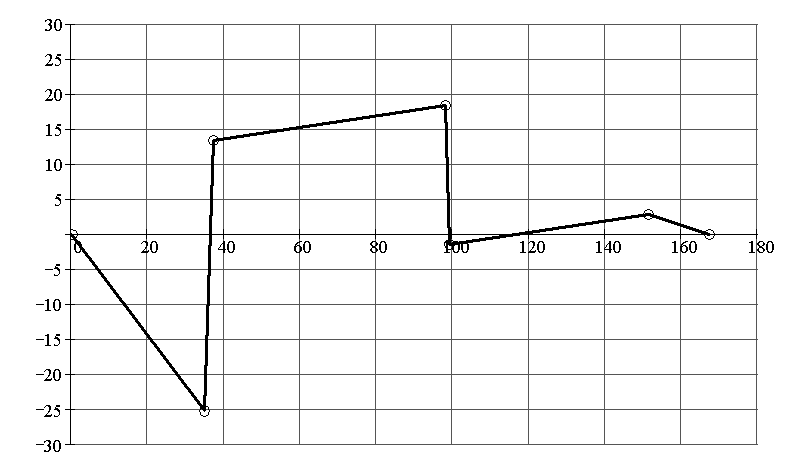
Примем потенциал точки А равным нулю и определим потенциалы остальных точек контура АВСДА. 

В 

В 

В 

В 

В 

В 

В 

f, В