Решение задачи формирования облика ракеты класса “воздух-воздух” на этапе предварительного проектирования, страница 5

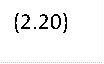
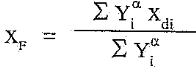
где Y₁ - подъемная сила той или иной части ЛА, X_di- координата точки приложения этой силы. На основании (2.20) для ЛА нормальной схемы найдем

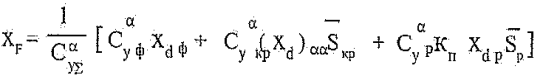
Можно показать [3], что степень продольной статической устойчивости ЛА зависит от взаимного положения его фокуса и центра тяжести.

Как следует из (2.22) степень продольной статической устойчивости m^Cy_z равна расстоянию между центром тяжести и фокусом, выраженному в долях корпуса. Преобразуя (2.22) найдем

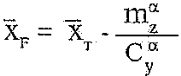
Вернемся теперь к выражению (2.15). Как видим, для расчета величин m^α_z и m^δ_z необходимо знать величины С^α_yф, С^α_yкр, С^α_yp и С^δ_yp   , которые нам уже известны из предыдущего. Кроме того необходимо дополнительно знать координаты центров давления Х_dф, Х_dкр, Х_dp.

В соответствии с методикой проф. Л.С.Чернобровкина величины X_dф   ,

X_dкр , X_dр определяются сначала для изолированных конструкций (крыльев, рулей, фюзеляжа), а затем вводится поправка на интерференцию. Что касается рулей, то поскольку они располагаются в конце корпуса, то их центр давления можно считать совпадающим с центром давления изолированного руля.

Определим теперь численные значения величин X_dф , X_dкр и X_dр для рассматриваемой компоновки.

1.  Центр давления изолированных крыльев. Линейная теория изолированных крыльев позволяет определить расстояние от начала САХ- x_dA до центра давления, отнесенное к величине хорды.

Для рассматриваемого крыла с λ_к   величина x_dA ≈ 0,4 (влияние увеличения угла атаки не учитываем).

2.  Центр давления изолированного фюзеляжа. Будем, как и ранее, учитывать лишь подъемную силу носовой части фюзеляжа. Согласно теории тонких тел вращения для малых чисел М

где    W     - объем носовой части корпуса. Для носовой части с параболическим обводом W_Hoc = 0,533 L_hoc S_M.

Опыт показывает, что при увеличении числа М центр давления смещается назад и тем больше, чем больше удлинение цилиндрической части корпуса. Величина дополнительного смещения в долях длины носовой части составляет  ∆Х/ L_нос = 0,45.

3.  Центр давления комбинаций "крылья-фюзеляж". Положение центра давления с учетом взаимного влияния крыльев и фюзеляжа для случаев "αα" и "δо" подробно рассмотрено в [3]. Мы на этом останавливаться не будем. Теперь перейдем непосредственно к формулировке второго условия. Из (2.16) при α_m = δ_m следует m_z^α = -m_z^α\. Полагая Х_т1 = 0,51; m_z^α= -0,08; X_т0 = 0,59 определим значение   m_z^α   приближенно принимая, что        Х_т1 ≈ (Х_dкр)_αα . Тогда, как следует из

Отсюда с учетом (2.3) найдем

Вертикальная прямая (2.26) приведена выше на рис. 2.2,б. Точка пересечения прямых (1) и (2) дает искомые значения S_Kp =6,2; S_р =3,2. Геометрическая схема ракеты с учетом полученных значений S_кр  , S_p и Х_кр ≈  1,8 приведена на рис.2.3_,а.

§3. Задача определения баллистических характеристик

Ракеты рассматриваемого типа являются одноступенчатыми и имеют однорежимный ракетный двигатель. В этом случае закон изменения скорости по времени включает два участка: стартовый и пассивный. Первый из них характеризуется малой продолжительностью (t =3÷5с) и резким нарастанием скорости полета (ускорение до 250 ÷300 м/с²). Второй участок соответствует свободному полету ракеты по инерции и характеризуется существенным изменением скорости. Рассмотрим методику определения баллистических характеристик ракеты V(t) и         S(t)= ^кʃ₀ V(t) dt. [2] Управление движения для стартового участка записано в виде:

Здесь R - тяга двигателя, X - сила лобового сопротивления. Пренебрегая в (З.1) влиянием силы лобового сопротивления и учитывая R = - gJ₁, m получим

Здесь J₁ - удельный импульс топлива. Интегрируя это уравнение с разделяющимися переменными в пределах: по времени - от нуля по t_r, но скорости - от начального значения V_H до максимального значения V_m получим формулу Цилковского

Определим прирост скорости за время стартового участка

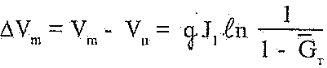
Зависимость относительного приращения, определенная из (3.4) приведена на рис.3.1,а сплошной линией.

Рассмотрим возможность упрощения формулы (3.4). Полагая

получим

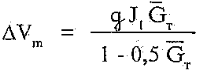
Соответствующая зависимость приведена пунктиром на рис,3.1,а. Физический смысл формулы (3.5) состоит в том, что прирост количества движения под действием импульса тяги определяется по среднему значению веса ракеты на стартовом участке G_n = G₀ (1- 0,5 G_T). Далее можно получить следующее приближение для формулы (3.4), соответствующее отказу от учета переменности массы.