Решение задачи формирования облика ракеты класса “воздух-воздух” на этапе предварительного проектирования, страница 2

6.   Размах рулей. Требование отсутствия складывания в отношении рулей обычно не ставится, что позволяет использовать рули с увеличенным размахом. Это увеличение размаха зависит от схемы складывания. Если складываемые части верхних и нижних рулей (см. рис.1.1,6) складываются навстречу друг другу и не выходят за пределы описанного по крылу квадрата, то очевидно

т.е. размах руля по сравнению с крылом увеличивается в  раза, что полезно с точки зрения увеличения удлинения руля.

7.  Форма крыльев и рулей в плане. На рассматриваемом этапе задача подробного выбора формы оперения (сужение, стреловидность) обычно не ставится. В целях упрощения дальнейшего исследования ограничимся рассмотрением крыльев и рулей прямоугольной формы (η=1). Отметим, что в реальных конструкциях такого оперения обычно вводят небольшую стреловидность по обеим кромкам

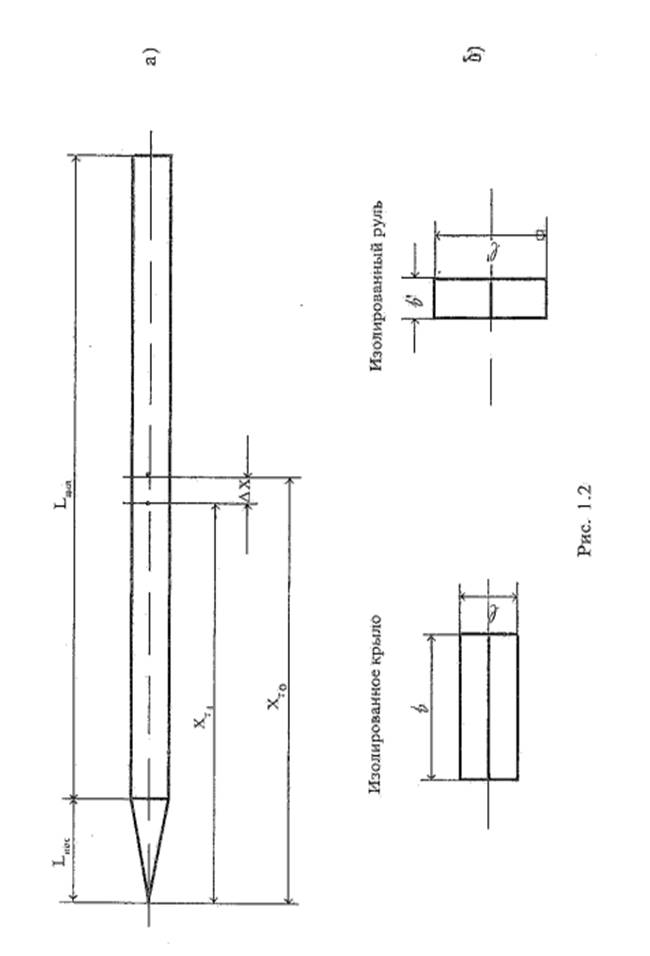
Перейдем теперь непосредственно к определению геометрии компоновки для ракеты со стартовым весом G_o=170 кг (см.рис.1.2). 

1.  Диаметр (калибр) корпуса ракеты. На основе имеющегося опыта проектирования ракет рассматриваемого класса диаметр корпуса может быть определен по следующей зависимости [1]

           (1.3)

где а = 0,1м, b=5,3- 10^-4 м/кг.  Из (1.3) получим, с учетом округления дот стандартизованных значений калибра D= 0,2 м.

2.  Длина корпуса ракеты. Выбор калибра ракеты заданного стартового веса однозначно определяет и длину корпуса ракеты. Пусть полная длина ракеты есть

                        (1.4) где Lнос - длина носовой части, Lнос - длина цилиндрической части ракеты. Величина Lнос в существенной степени зависит от типа головки самонаведения (ГСН), используемой на ракете. Так для радиолокационных головок самонаведения оптимальное значение удлинения носовой части с параболическими обводами

λ_нос= L_нос / D

составляет ~ 2,5 , для тепловых головок самонаведения это значение может снижаться до 0,5 (полусфера). В дальнейшем ограничимся рассмотрением ракеты с радиолокационной ГСН и примем λ_нос = 2,5. Полагая далее, что вес ракеты G_o равномерно распределен по цилиндрической части корпуса (носовая часть корпуса, крылья и оперение весят мало) получим

                      (1.5)

 

где: γр[кг/м³]- средняя плотность цилиндрической части ракеты [1],       S_м=π D²\4- площадь миделевого сечения корпуса.

Отсюда для G₀ = 170 кг; S_M = 0,0314 м²; γ_р=1,75-10³кг/м³ найдем Lцил = 3,1 м. С учетом длины носовой части L_нoc=2,5∙0,2 = 0,5м. полная длина ракеты составит 3,6 м.

3.  Начальное положение центра тяжести ракеты X_т0 – есть расстояние от носка ракеты до ее центра тяжести в стартовом состоянии. Очевидно,

X_т0  =L_нос+L_цил /2              (1.6)

С учетом Lнос= 0,5 ; Lцил = 3,1 получим  Х_т0=2,05 м.

4.  Конечное положение центра тяжести ракеты Х_т1 Процесс горения стартового заряда сопровождается смещением центра тяжести вперед к носку корпуса. При полном выгорании топлива величина смещения ∆Х = Xт0 - X определяется выражением (см.рис. 1.2,а)

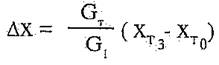    (1.7)

где: G_T,  X_T3    - вес и координата центра тяжести порохового заряда, G1 = Ст₀ - G_T - конечный вес ракеты. На основании (1.7) при G_T = 60 кг, G1 =110 кг, X_т3 = 2,4 м  получим ∆Х=0,2м, Х_Т1 = Х_Т0- ∆Х = 1,85 м.

5.  Геометрия оперения ракеты. Будем рассматривать компоновку ракеты с крылом сверхмалого удлинения и складываемыми рулями.

1)  Геометрия крыла.   Выше было  показано,  что  допустимый размах крыла определяется величиной стороны описанного квадрата - а. Примем а = 0,35 м. Тогда при D =0,2 м получим величину размаха консоли крыла

Поскольку геометрические параметры   консоли крыла (площадь, размах, удлинение) связаны известной зависимостью

                 ( 1.8 )

а величина размаха консоли фиксирована £_к= 0,3 м, из (1.8) получим связь между площадью консоли крыла – S_кр    и удлинением консоли крыла

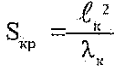                (1.9)

Для дальнейшего удобно оперировать относительными параметрами. Будем далее относить линейные размеры к длине корпуса  L=3,6м и площади миделевого сечения S_м = 0,0314м². Тогда из (1,9) получим

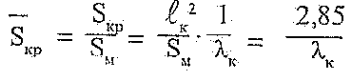                (1.10)

Зависимость  S_кр(λ_к)  приведена на рис.1.3,а.  Как видим при S_Kp = б удлинение консоли крыла не должно превышать λ_к = 0,5.

2)   Геометрия руля. По аналогии с (1.10) имеем

     (1.10)