Решение задачи формирования облика ракеты класса “воздух-воздух” на этапе предварительного проектирования, страница 4

Указанные составляющие суммируются суперпозитивно. Кроме того при их объединении должен быть учтен эффект-взаимодействия (интерференции). В соответствии с методикой проф. Л.С. Чернобровкина при определении подъемной силы комбинаций “крыло-корпус” и “руль-корпус” необходимо на коэффициент интерференции.

Определим численные значения указанных составляющих подъемной силы. Первая и третья составляющие для прямоугольных конфигураций могут быть определены по единой формуле, учитывающей влияние концевого эффекта. Производная подъемной силы изолированного оперения по углу атаки может быть определена по формуле

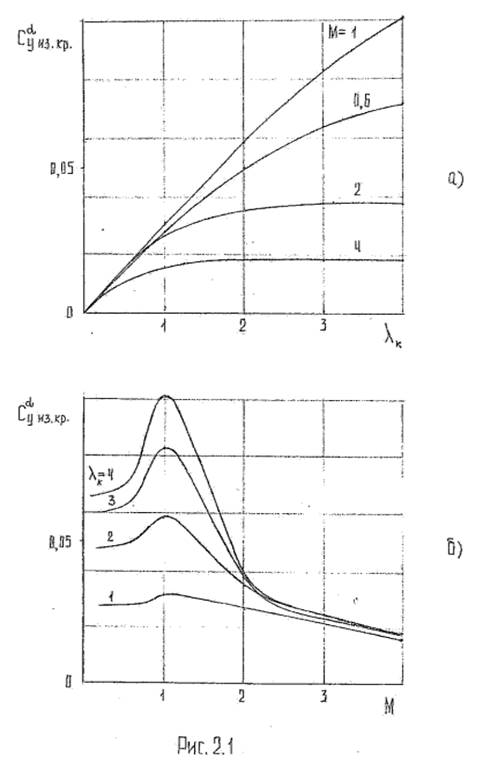
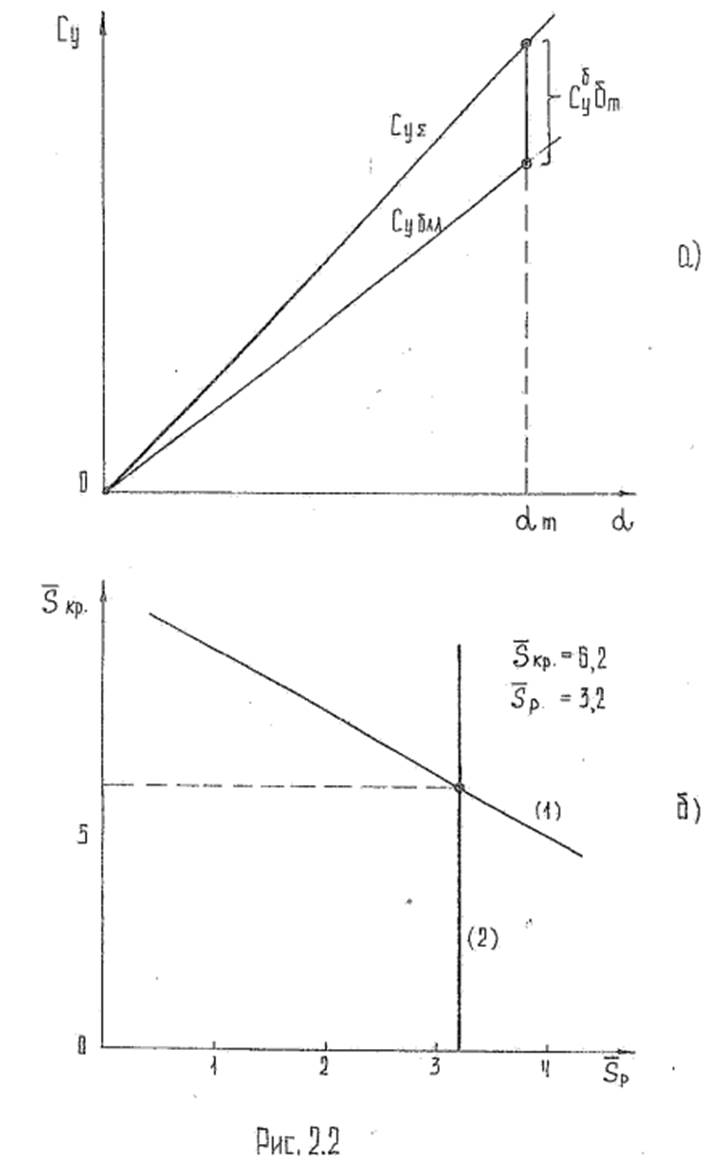
Зависимость С_{y из.кр}  в функции λ_к и М приведена на рис. 2.1,а,5.

Из (2.2): С_y^α_из.кр. = 0,0163; С_y^α_из.р = 0,024.

Вторая составляющая определяется в основном носовой частью фюзеляжа  (с учетом цилиндрической части) С_y^α_нос =0,06. Относя полную подъемную силу к площади миделя сечения S_M и к скоростному напору, получим:

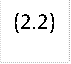 где: К =0,9 учитывает торможение потока за крылом, коэффициенты интерференции для крыла и руля - К_αα′ = 1,94; К_αα′′= 1,68.

Для   определения   балансировочного   значения   С_yбал^α нам потребуется значение С_y^δ. Имеем:

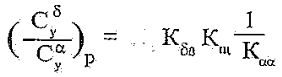
где К_щ = 0,85 - коэффициент, учитывающий влияние щели; K_δ0   -  коэффициент интерференции для случая "δ0" [4].

На основании (2.3) и (2.4) при D= 0,285 К'_αα = 1,68; K_δ0= 1,24; К_щ = 0,85

получим

Оценим теперь балансировочное значение коэффициента подъемной силы по углу атаки при α_m= δ_m = 20° с учетом потери подъемной силы при отклонении рулей (см. рис.2.2,a).

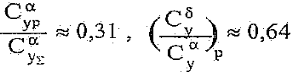
Из соотношения (2.8) и с учетом обеспечения требуемого значения располагаемой перегрузки в контрольном режиме n_y =3,0 найдем связь между искомыми параметрами S_кр и S_р . Учитывая

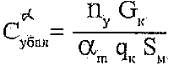
получим из (2.8) и (2.9) с учетом G_K = 110 кг, q_к= 1620 кг/м², α_m- 20°, S_м= 0314m^s

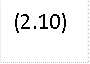
Зависимость (2.10) приведена на рис. (2.2,б). Теперь перейдем к рассмотрению второго условия.

2. Балансировка ракеты. Для определения балансировки ракеты нам необходимо рассмотреть зависимость m_z1 (α,δ) в связанной системе координат. Безразмерный  коэффициент момент определяется выражением

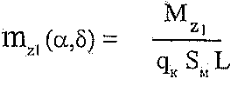
Здесь, как и ранее, S_M и L - площадь миделя и длина корпуса ракеты. Для определения момента аэродинамических сил относительно оси OZ₁ необходимо знать величины этих сил и точку их приложения. Составим выражение продольного момента всего летательного аппарата относительно оси OZ₁ , проходящей через его центр тяжести. Этот момент представляет собой алгебраическую сумму моментов создаваемых фюзеляжем, крыльями и рулями. Таким образом суммарный момент:

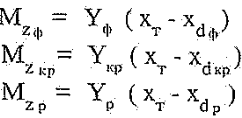
Здесь х_{т –} координата центра тяжести, х_dф, х_dкр, х_dp – координаты центров давления фюзеляжа, крыла и руля, отсчитываемые от носка ракеты. Подставляя равенства (2.13) в выражение (2.12) и переходя к безразмерным коэффициентам получим:

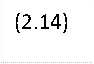
Отсюда получим с учетом m_z0 = 0

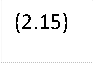
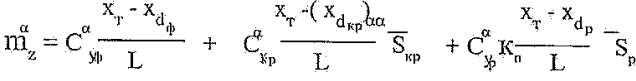
С учетом (2.15) выражение (2.14) может быть представлено в виде

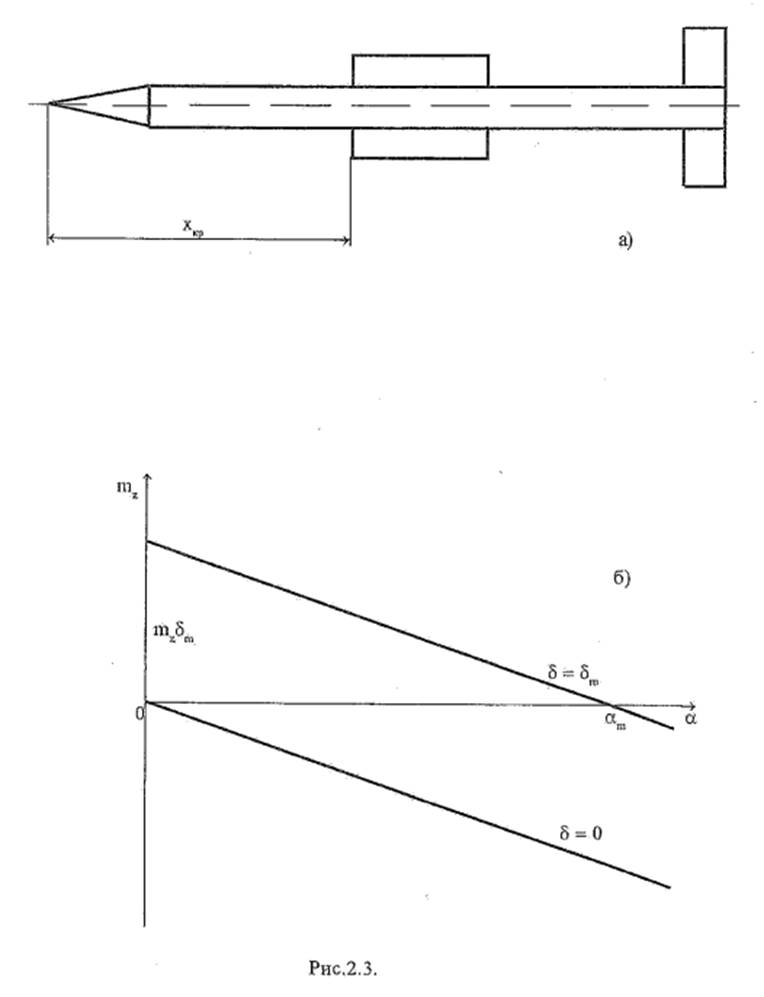
Зависимость (2.16) приведена на рис.2.3,б. Отметим, что для статически устойчивого летательного аппарата

Производная (ш )_бял , от которой зависит абсолютная величина восстанавливающего момента называется степенью продольной статической устойчивости.   Так как С  и а   связаны в большинстве случаев линейной зависимостью, то наряду с кривыми 1X1. (а) строят кривые ТТ\( С,). Частная производная ( Ш ру)      как и производная ( m^a ) дает качественную и количественную оценку статической устойчивости летательного аппарата и поэтому также называется степенью (запасом) продольной статической устойчивости. Эти производные связаны между собой равенством

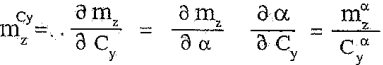                      (2.18)

Остановимся еще на понятии фокуса симметричного летательного аппарата. Выше было показано, что подъемная сила ЛА может быть представлена в виде суммы двух слагаемых, одно из которых пропорционально углу атаки, второе пропорционально углу отклонения рулей.

Каждая из составляющих подъемной силы приложена в определенной точке. Назовем фокусом летательного аппарата точку приложения той части подъемной силы, которая обусловлена углом атаки. Как видно из данного определения фокус в общем случае не совпадает с центром давления ЛА, т.е. с точкой приложения всей подъемной силы. Только в одном частном случае, а именно при δ'= 0 и полной симметрии ЛА, когда Y = Y^α α центр давления совпадает с фокусом. Обозначим продольную координату фокуса, измеренную от носка ракеты через X_F. Так как фокус представляет собой точку приложения равнодействующей подъемных сил, обусловленную углом атаки, то