В технологии микроэлектроники используют плоскопараллельные пластины, глубина проведения процессов диффузии много меньше толщины пластин. Это означает, что для теоретического анализа можно ограничиться одномерным случаем. При этом если концентрация примеси изменяется лишь в одном направлении, то выражение для потока в некоторой точке с координатой xв момент времени tбудет иметь вид
.
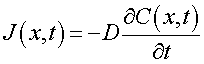С учетом закона сохранения вещества из первого закона Фика можно вывести выражения для второго закона Фика, согласно которому изменения концентрации вещества в некотором объеме должно определяться потоком внутрь этого объема:
(4.2)
или для одномерного случая
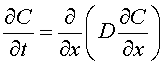(4.3)
Уравнение (4.3) называют уравнением диффузии, его решение для конкретных граничных условий описывает характер распределения диффундирующих частиц в различных точках среды в зависимости от времени.
Традиционно термодиффузионные процессы в технологии микроэлектроники проводят в две стадии. На первой стадии на поверхности подложки формируют тонкую легированную область. На второй стадии при отжиге структуры в атмосфере, не содержащей примесей, добиваются перераспределения введенных на первой стадии примесей в подложку. Первая стадия традиционного диффузионного процесса соответствует случаю диффузии в полубесконечное тело из бесконечного источника, вторая стадия процесса - диффузии в полубесконечное тело из ограниченного источника.
Рассмотрим решение уравнения диффузии для этих двух случаев.
Диффузия в полубесконечное тело из бесконечного источника
Полубесконечным телом любую монокристаллическую пластину можно считать при условии, что диффузия проводится на глубину, много меньшую толщины подожки. Бесконечным (или постоянным) источником называют такое состояние системы, когда количество примеси, уходящей с поверхности в объем полупроводника, равно количеству, поступающему на поверхность. Это означает, что количество примеси вокруг пластины, например в газовой фазе, значительно больше, чем в ее объеме.
В этом случае граничные условия записываются как С(x, t) = 0 при t = 0;
C(x,0) = C0 при t> 0,x = 0.
Решение уравнения (4.3) при данных граничных условиях описывается дополнительной функцией ошибок
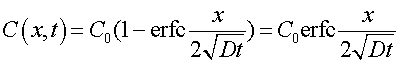. (4.4)
Количество примеси, введенное в подложку за время диффузии из бесконечного источника Qt, определяется как
.
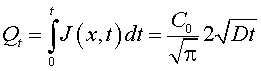(4.5)
Коэффициент диффузии D– величина, экспоненциально зависящая от температуры:
, (4.6)
где Еa– энергия активации диффузии, эВ; k– постоянная Больцмана, 8,6×10-5 эВ/К; Т – температура, К.
Если в объеме подложки присутствует другая примесь с концентрацией CB, то суммарное количество примеси СS будет равно
,
(4.7)
при этом знак минус соответствует случаю, когда примесь в подложке и вводимая примесь имеют разный знак, т.е. формируется гетеропереход. Глубина залегания p-nперехода определяется условием
или (см. рис. 4.1)
.
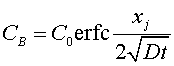(4.8)
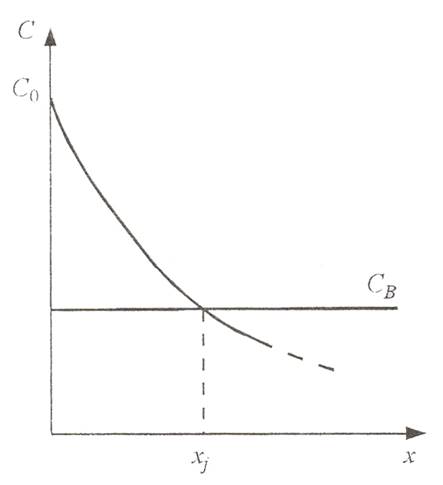
Рис. 4.1 Характер распределения донорных примесей в подложке с концентрацией акцепторов СВ.
Диффузия в полубесконечное тело из ограниченного источника
Этот случай соответствует условиям, когда в тонком приповерхностном слое создана избыточная концентрация примеси С0, количество которой непрерывно уменьшается в процессе термообработки, тогда как концентрация примеси на глубине постепенно увеличивается.
Граничные условия в этом случае можно представить в виде
С(x,0) = С0 при t=0, x = 0;
С(x,t) = 0 при t ¹ 0, x ®¥.
При этом решение уравнения диффузии имеет вид функции Гаусса
.
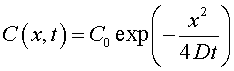(4.9)
Изменение поверхностной концентрации зависит как от температуры процесса, так и от его продолжительности:
Глубина залегания p-nперехода при диффузии в подложку с концентрацией примесей СB определяется аналогично (4.8):
.
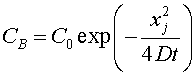Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.