Прогнозирование возможности и характера процесса эпитаксии. Диффузия в полубесконечное тело из ограниченного источника, страница 4

В дальнейших расчетах учитывают не все возможные соединения кремния. Для упрощения вычислений компонентами, имеющими парциальные давления ниже 0,1 Па, пренебрегают (например, SiH, Si₂, Si₃, Si₂Cl₆, SiCl). Для оставшихся компонентов газовой фазы определяют число независимых химических реакций, которое равно разнице между числом компонентов в системе в целом rи числом атомов в этой системе e:

.

Например, если для термодинамического анализа отобраны компоненты SiCl₄, SiHCl₃, SiH₂Cl₂, SiH₃Cl, SiCl₂, HC1, H₂, то с учетом конденсирующегося кремния r= 8, е = 3 и для проведения термодинамического анализа требуется пять линейно независимых реакций, т.е. таких, которые не могут быть получены линейной комбинацией других (сравните с уравнениями (3.1)).

Например:

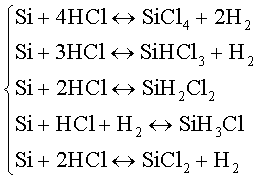                                       (3.4)

Пять уравнений закона действующих масс для этих реакций составят систему пяти уравнений с семью неизвестными парциальными давлениями. Систему уравнений дополняют уравнением постоянства давления в системе Si – Н – С1 и условием постоянства соотношения давлений неконденсируемых атомов x = const, характерным для изобарических процессов. Это означает, что величина xна входе в реактор, равная 4m/2(100 - m), при заданной концентрации тетрахлорида кремния в исходной ПГС, равной m%, не изменится и в реакционной зоне (см. (3.2), (1.3)) и будет равна величине xна выходе из реактора:

.

Таким образом, система уравнений примет вид

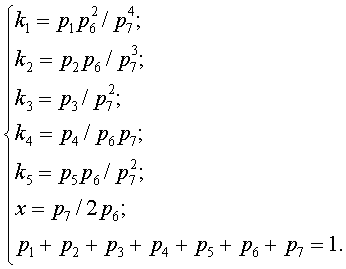
Это позволит определить равновесные парциальные давления компонентов газовой фазы через заданное значение x, известные значения констант и парциальное давление одного из компонентов, например, через p₇:

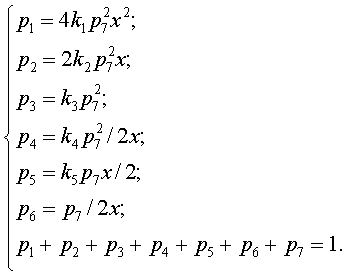                  (3.5)

или

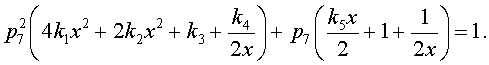                        (3.6)

Итоговое квадратное уравнение (1.6) относительно p₇ позволяет определить парциальные давления p₁ ¸ p₆, а по полученным значениям p₁ ¸ p₇ рассчитать равновесный выход кремния в процессе b, который определяется как отношение количества атомов кремния в конденсированной  фазе к исходному количеству в ПГС :

.

Если число атомов кремния в момент равновесия считать равным , то в конденсированной фазе окажется и

, тогда

.

Число атомов кремния в исходной ПГС удобно выразить через соответствующее количество атомов Cl (например, для тетрахлорида кремния на 1 атом кремния приходится 4 атома хлора), так как последний не конденсируется и

, а

 или                                (3.7)

где

.

Очевидно, что если в равновесной ПГС у < 0,25, то происходит осаждение кремния, если же у > 0,25, - травление кремния.

Результаты термодинамического анализа представляют в виде номограмм (например, рис. 3.1) или зависимостей парциальных давлений компонентов газовой фазы от температуры, давления, параметра xи т.п.

Однако далеко не всегда эпитаксиальный процесс описывается равновесной реакцией. Поэтому необходимо учесть, что расчеты равновесной термодинамики указывают лишь на наиболее вероятную картину. В табл. 3.2 приведены результаты расчетов равновесного парциального давления компонентов газовой фазы для суммарного давления в системе 1 атм и для x = 0,1.

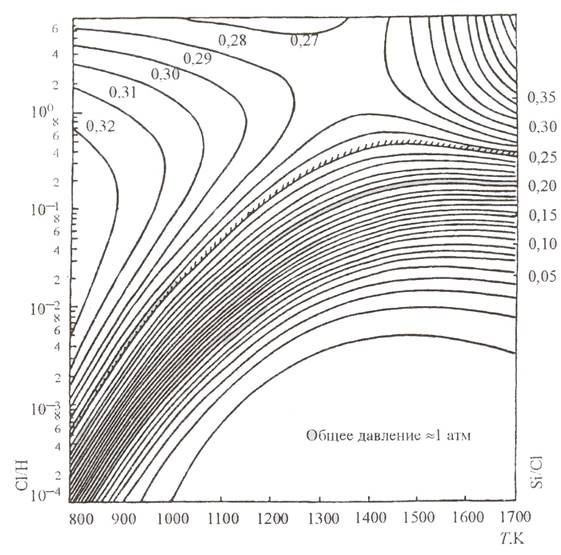
Рис.3.1 Обобщенные результаты термодинамического анализа системы Si – Cl – H

Расчет технологических параметров процесса диффузии

Если рассматривать диффузию как процесс переноса атомов в неравновесной системе, вызываемый только наличием градиента концентрации вещества, то выражение для потока вещества, проходящего в единицу времени через единицу площади сечения перпендикулярно направлению перемещения вещества, характеризуется следующим уравнением:

                                                 (4.1)

где J – поток диффундирующего вещества; D– коэффициент пропорциональности, называемый коэффициентом диффузии, см²/с; С – концентрация атомов вещества, см^-3.

Знак минус в уравнении означает, что поток атомов (и, следовательно, сам процесс диффузии) направлен в сторону убывания концентрации примеси.

Уравнение (4.1) называют первым законом Фика (по имени швейцарского физика, получившего его), согласно которому локальная скорость диффузии через сечение единичной площади в единицу времени пропорциональна градиенту концентрации растворенного вещества, а направлена диффузия в сторону убывания концентрации примеси.