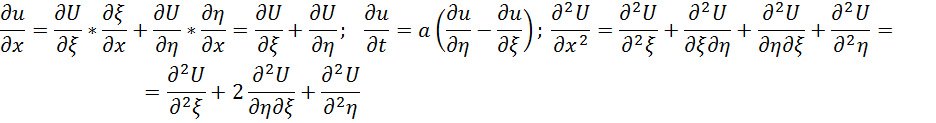
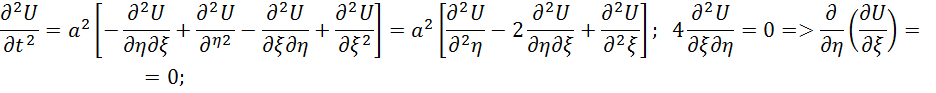
Частная по η=0 значит
не зависит от η 
проинтегрируем последнее уравнение
это самое общее решение уравнения 1
оно называется решением Даламбера
16 Решение Фурье
17 Уравнение распространения тепла в стержне 
18 Распространение тепла в пространстве – опытным путём установлено что количество тепла протекающего через площадку ΔS равно: ΔQ =-k(𝜕U/𝜕n)ΔS. Количество тепла протекающего через всю поверхность ΔQ*Δt=-k*gradU*n*ΔSΔt
19 Численное решение уравнения распространения тепла в стержне методом конечных разностей
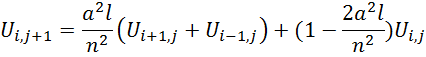
Данная формула справедлива, если l≤
если шаг подобрать так чтобы скобка 
то формула примет
вид:
20 Задача приводящая к исследованию уравнений Лапласа – формулировка краевых задач
1) Стационарное
распределение температуры в однородном теле 
1. Если известна температура поверхности тела т.е. U=φ(x), То такая задача называется задачей диракля или первой краевой
2. Если известен тепловой поток в каждой точке поверхности, который пропорционален
то задача называется второй краевой
или задачей Кеймана.
2) Потенциальное
течение жидкости или газа 
Теория функции комплексной переменной
22 Комплексные числа. Алгебраическая и тригонометрическая форма записи. Действия над комплексными числами - комплексным числом называется выражение вида z=x+iy(алгебраическая форма записи), где i мнимая единица.
1. Сложение и вычитание
2. Умножение
3. Деление
Cosnφ+icosnφ – тригонометрическая форма записи
23 Элементарные функции комплексной переменной – элементарной функцией комплексной переменной называют функции, которые получаются из элементарных функций вещественной переменной, определяемых разложением в степенной ряд по следующему правилу, если z=t(x)=a0+a1x+…+anxn+… - элементарная функция вещественной переменной х, то w=f(z)=a9+a1z+…+anzn+… - элементарная функция комплексной переменной z очевидно, что функция определяется лишь для таких значений комплексной переменной при которой ряд сходится.
1. Степенная функция W= Zn Степенная функция определена для всех комплексных чисел. Каждому комплексному числу она ставит соответствие Zn т.е. произведение n-множителей каждый из которых равен n. Данная функция обладает свойствами вещественного переменного
2. Показательная функция
24 Производная функции комплексной переменной Условие Коши-Мимона
25 Геометрический смысл производной функции комплексного переменного
26 Интегрирование по комплексному аргументу
27 Свойства криволинейного интеграла. Теорема Коши. Формула Ньютона – Лейбница
28 Формула Коши (2 следствия)
29 Степенные ряды с комплексными числами
30 Изолированные особые точки и их классификация
31 Ряд Лорана. Вычиты
32 Операционные исчисления. Преобразования Лапласа
33 Свойства преобразований Лапласа
34 Свёртка функций. Теорема об умножении изображения. Интеграл Дюамеля
35 Таблица некоторых преобразований Лапласа
36 Формула обращения
37 Оригиналы с рациональными изображениями
38 Теория вероятности. Классическое определение вероятности. Свойства вероятности
39 Основные свойства комбинаторики
40 относительная частота
41 Теоретические вероятности
42 Теорема сложения вероятностей
43 Теорема умножения вероятностей
44 Независимые события
45 Теорема сложения вероятностей совместных событий
46 Формула полной вероятности
47 Вероятность гипотез
48 Формула Бернулли
49 Локальная теорема Лапласа
50 Интегральная теорема Лапласа
51 Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
52 Случайные величины, дискретные и непрерывные случайные величины
53 Закон распределения вероятности дискретной случайной величины
54 Биномиальное распределение
55 Числовые характеристики случайной величины. Математической ожидания, его свойства
56 Дисперсия случайной дискретной величины
57 Среднеквадратичное отклонение суммы независимых случайных величин
58 Одинаково распределённые независимые случайные величины
59 закон больших чисел
60 функция распределения вероятностей случайной величины
61 Плотность распределения вероятности случайной величины
62 Числовые характеристики непрерывных случайных величин
63 Равномерное распределение
64 Показательное распределение
65 Нормальное распределение
66 Вероятность попадания в интервал нормальной случайной величины
67 вычисление вероятности заданного отклонения для нормально распределённой случайной величины
68 Задача математической статистики
69 Генеральная и выборочная совокупность
70 Способы отбора
71 Статистическое распределение выборки
72 Эмпирическая функция распределения
73 Полином и гистограмма
74 Статистическая оценка параметров распределения
75 Генеральная и выборочная средняя. Оценка генеральной средней по выборочной средней
76 Групповая и общая средняя
77 Генеральная дисперсия, выборочная дисперсия
78 оценка генеральной дисперсии по исправленной выборочной
79 Точность и надёжность оценки. Доверительный интеграл
80 Доверительный интервал для оценки математического ожидания нормального распределения при известном δ
81 Оценка биноминального распределения по относительной частоте
82 интервальная оценка
83 Эмпирические моменты
84 Метод моментов для точной оценки параметров распределения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.