1 Булевы функции – это функции которые принимают только два знака 0 или 1 а х, х1, х2,…хn выступают в роли набора нулей и единиц, зависит от любого количества переменных, эту функцию можно задать таблицей истинности
2 Свойства булевых функций – 1)конъюнкция, дизъюнкция, сумма по модулю 2, стрелка Пирса, штрих Шэйфера – обладают свойством коммутативности
2) конъюнкция, дизъюнкция, сумма по модулю 2 обладают свойствами ассоциативности и дистрибутивности [а или (b или c) = (a или b) или с a или (b и c)=(a или b) и (a или c)]
3)Закон ДеМоргана [ не (a и b)= (не a) или (не b) не (a или b)=(не a) и (не b)]
4) Закон двойного отрицания [не(не a) = a]
5) выражение дизъюнкции через конъюнкцию и сумму по модулю 2[a или b= a и b +2 b +2 a]
6) выражение дизъюнкции через импликацию [ a v b =(a->b)->b]
7)выражение отрицания через | , ↓, ↔, +2 [не а =a|a, a ↓ a, a+21, a↔0]
8) выражение конъюнкции через | [a и b =(a|b)|(a|b)]
9) выражение дизъюнкции через ↓ [a v b=(a↓b) ↓(a↓b)
10)закон поглощения [a и b или a = a]
11) закон склеивания [не а или а = не а +2а =1]
12) для функций конъюнкция, дизъюнкция, сумма по модулю 2 справедливы тождества
|
а и а = а Не а и а =0 а и 0 = 0 а и 1 = а |
А или а =а Не а или а = 1 А или 0 = а А или 1 = 1 |
а+2 а = 0 а +2 не а = 1 а +2 0 = а а +2 1 = не а |
3 Двойственность – Пусть функция f( x1, x2,…, xn) – булева функция, f*(x1, x2,…, xn) является двойственной если f*(x1, x2,…, xn) = f(не x1, не x2,…, не xn) функция называется самодвойственной если f*=f
4 Дизъюнктивные и конъюнктивные нормальные формы – конъюнктивным одночленом от переменных х1, х2,… хn называется конъюнкция этих переменных или их отрицаний
Аналогично для дизъюнктивного одночлена
5 СДНФ и СКНФ – СДНФ – это ДНФ , в которой каждый конъюнктивный одночлен, каждая переменная Xi из набора f’(x1, x2,…, xn) входит ровно 1 раз причём либо сама либо её отрицание
СКНФ – это КНФ которая удовлетворяет следующим условиям
1. КНФ не содержит 2-х одинаковых дизъюнкций
2. Ни одна из дизъюнкций не содержит одновременно некоторую переменную и её отрицание
3. Ни одна из дизъюнкций не содержит одновременно 2-х одинаковых переменных
4. Каждая дизъюнкция СКНФ содержит либо переменную либо её отрицание, для всех переменных входящих в формулу
6 Многочлен Жегалкина – называется многочлен являющийся суммой константы и различных одночленов в которые каждая переменная входит невыше чем в 1-ой степени. Многочлен Жегалкина константы равен самой константе
7 Логические исчисления - оперируют высказываниями. Высказывание – повествовательное предложение о котором в данной ситуации можно сказать, что оно истинно или ложно, но нито, ни другое одновременно
8 Логические отношения – иногда бывает желательно рассмотреть взаимоотношение 2-х высказываний. Наиболее интересное из таких соотношений имеет место когда из одного высказывания логически следует другое. Если X следует Y, то говорятч то Y является следствием Х. Отношение следствия можно охарактеризовать таким образом: из Х следует Y если Y истинно всякий раз, когда истинно Х, т.е. если y истинно во всех логических возможных случаях в которых Х истинно. В случае составных высказываний, имеющих одни и теже компоненты, таблицы истинности дают удобный метод для проверки того, имеют ли место соотношения следствия.2 высказывания называются не совместимыми, если из одного следует ложность другого
9 Варианты импликации
|
XY 00 01 10 11 |
НеX неY 11 10 01 00 |
X→Y 1 1 0 1 |
Y→X 1 0 1 1 |
Не X→не Y 1 0 1 1 |
Не Y→не X 1 1 0 1 |
10 Осн. законы определяющие свойства логич. операций
1. Х или Х ↔ Х, Х и Х ↔ Х
2. Коммутативность конъюнкции и дизъюнкции
3. Ассоциативность конъюнкции и дизъюнкции
4. Дистрибутивность операций конъюнкции и дизъюнкции
5. Двойное ортицание
6. Закон ДеМоргана
7. Склеивание
8. Поглощение
9. Действия с логическими константами
10. Закон исключения 3-го
11. Х↔Х
12. Отрицание противоречий
13. Контропозиция
14. Ценное заключение
15. Противоположность
16. (Х и(Х →Y))→Y↔1
11 Предикаты – функция значениями которой высказывания о «n»-обьектах представляющих значения аргументов
12 Кванторы – Квантор общности - это оператор, приводящийся в соответствие любому заданному предикату Y=P(x) такую двузначную логическую переменную Z, которая принимает значение 1 тогда и только тогда, когда Y=1 при всех значениях Х.
Квантор существования – это оператор приводящий в соответствие любому одноместному предикату Y=P(x) такую двузначную логическую переменную Z каторая принимает значение ) тогда и толь ко тогда, когда Y=0 при всех значениях Х
13 Действия над кванторами
1. Перенос квантора через отрицание
2. Вынос квантора за скобки
3. Перестановка одноимённых кванторов
4. Переименование связанных переменных
14 Уравнения математической физики. Уравнение колебания струны – под струной понимается тонкая нить, которая может свободно изгибаться. Если струну вывести из состояния равновесия а затем предоставить самой себе, то струна начнёт колебаться
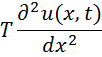
15 Решение Даламбера – Рассмотрим случай свободных колебаний
бесконечной струны. Искомая функцияU(x,t) должна удовлетворять уравнению 
(1)и начальным условиям U(x,0)=φ(x) (2) и 
.
Так как струна неограниченна, то функции φ(х) и 𝜓(х)
должны быть заданы в промежутке ( -∞; ∞) Найдём самое общее решение уравнения
(1). Преобразуем уравнение (1) к новым независимым переменнымξ=x-at, η=x+at
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
