Анализ системы автоматического регулирования

Министерство образования и науки Российской Федерации

Иркутский государственный технический университет

Кафедра электрических станций сетей и систем

Курсовой проект

по дисциплине ТАУ:

«Анализ САР»

Выполнил: студент группы АР-06-1

Азорин А. Ю.

Проверил: преподаватель

Новожилов М. А.

Иркутск 2009

План курсовой работы:

1.  Схема САР, математическое описание элементов__________1

2.  Преобразование структурной схемы_____________________3

3.  Определение Кир с помощью метода D-разбиений_________4

4.  Частотные характеристики_____________________________5

5.  Устойчивость САР____________________________________9

6.  MATLAB-модель САР________________________________12

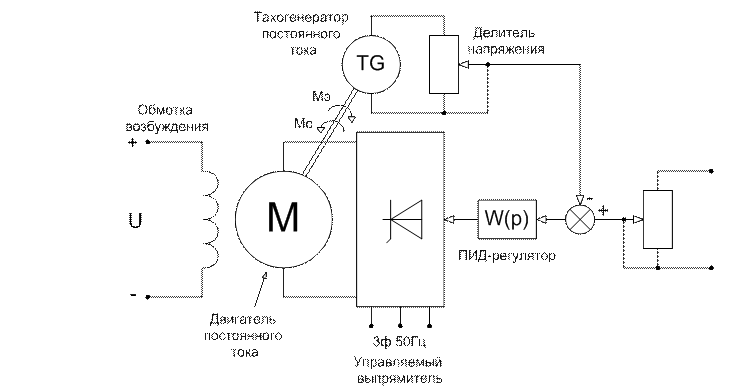
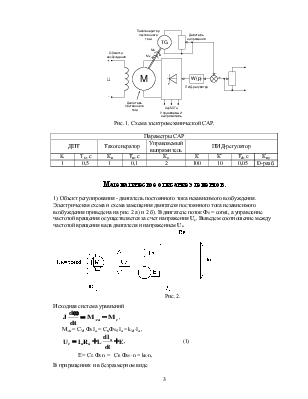
Рис. 1. Схема электромеханической САР.

Параметры САР
ДПТ		Тахогенератор		Управляемый выпрямитель	ПИД-регулятор
K	Tв, с	Ки	Ти, с	Кр	К	К`	Тd, с	Кир
1	0,5	1	0,1	2	100	10	0,05	D-разб.

Математическое описание элементов.

1) Объект регулирования - двигатель постоянного тока независимого возбуждения.

Электрическая схема и схема замещения двигателя постоянного тока независимого возбуждения приведена на рис. 2 а) и 2 б). В двигателе поток Ф_d = const, а управление частотой вращения осуществляется за счет напряжения U_с. Выведем соотношение между частотой вращения вала двигателя и напряжением U_с.

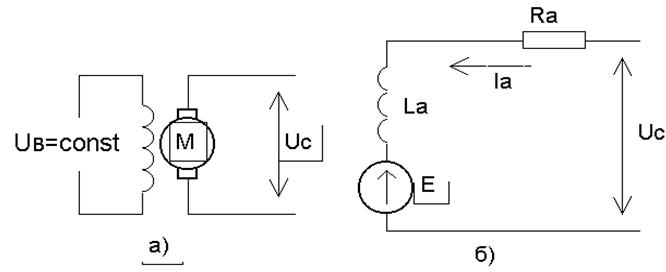
Рис. 2.

Исходная система уравнений 

      ,                              

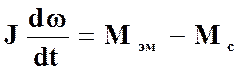      М_эм = С_М Ф_d I_а = С_мФ_d0×I_a = k_M×I_a ,         

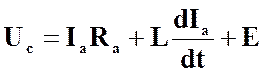      ,                                        (1)

                 Е = С_Е Ф_d n =   С_E Ф_d0 ×n = k_E×n,                

В приращениях и в безразмерном виде

          

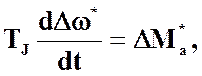
           ,                                                   (2)

            .

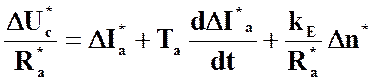Пренебрегая электромагнитной постоянной времени якоря Т_а, поскольку она на много меньше постоянной инерции Т_J, подставив последние уравнения системы (2) в первое уравнение получим:

.

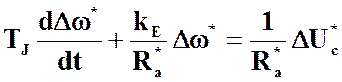Разделим полученное уравнение на , получим

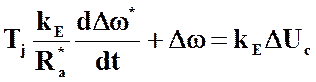,    (3)

Уравнению (3) соответствует передаточная функция объекта регулирования:

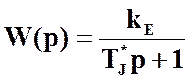,        (4)

где .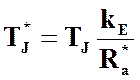

2) Измерительный элемент  - тахогенератор постоянного тока.

Тахогенератор в электромеханических системах регулирования применяется для преобразования частоты вращения вала в напряжение постоянного тока, пропорциональное частоте вращения. Тахогенератор представляет собой машину постоянного тока с возбуждением от постоянных магнитов.

Дифференциальное уравнение, описывающее тахогенератор можно представить уравнением

,    (5)

где:

Т_и  - постоянная времени, определяемая индуктивностью и активным сопротивлением якорной обмотки тахогенератора;

k_и  - коэффициент усиления;

U_и – выходное напряжение тахогенератора,

n – измеряемая частота вращения.

Уравнению (5) соответствует передаточная функция

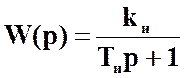.          (6)

3) Усилитель мощности – тиристорный преобразователь

Для усиления сигнала по мощности от регулятора используется симметричный управляемый тиристорный преобразователь, собираемый по трехфазной мостовой схеме (схема Ларионова). Если пренебречь запаздыванием в системе сеточного управления моста, то соотношение между сигналом, подаваемого на систему сеточного управления моста U_вх с выхода регулятора и выходным напряжением моста U_вых можно упрощено описать уравнением

U_вых = к_тр U_вх ,        (7)

где  к_тр – коэффициент усиления управляемого тиристорного моста.

4) ПИД – регулятор.

Уравнение стандартного ПИД  - регулятора

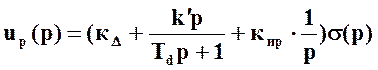 ,          (8)

где: u_р – выход регулятора,

s - входная величина регулятора (ошибка регулирования),

к_D, к¢, к_и – коэффициенты регулирования по отклонению, производной, интегральной составляющей входной величины регулятора соответственно,

Т_d – постоянная времени в канале производной,

р – оператор дифференцирования.

Преобразование структурной схемы.

Рис. 3. САР с единичной обратной связью.

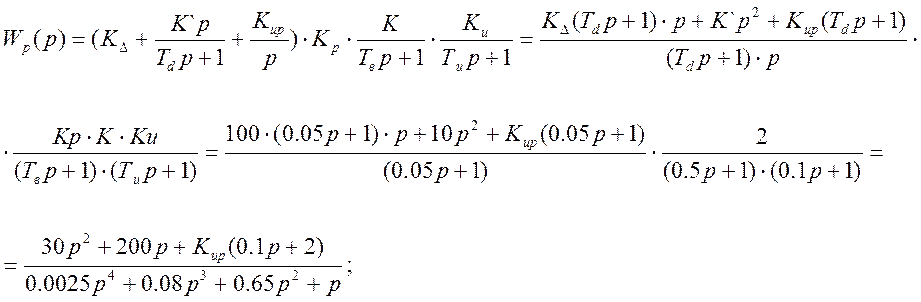Передаточная функция разомкнутой САР:

Передаточная функция замкнутой САР:

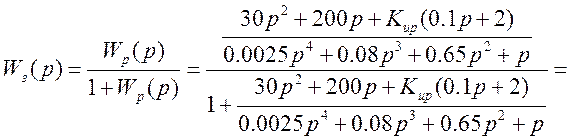
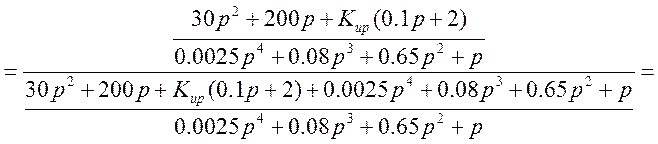
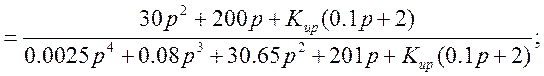
Характеристическое уравнение разомкнутой САР:

Характеристическое уравнение замкнутой САР:

Определение К_ир с помощью метода D-разбиений.

D-разбиение выполняется с целью определения значений настроечных параметров (в основном это параметры регулятора), обеспечивающих наибольший запас устойчивости САР.

 Процедура D-разбиения состоит в том, что определяется  характеристическое уравнение замкнутой САР, в котором выделены настроечные параметры, а все остальные параметры САР заданы численными значениями.

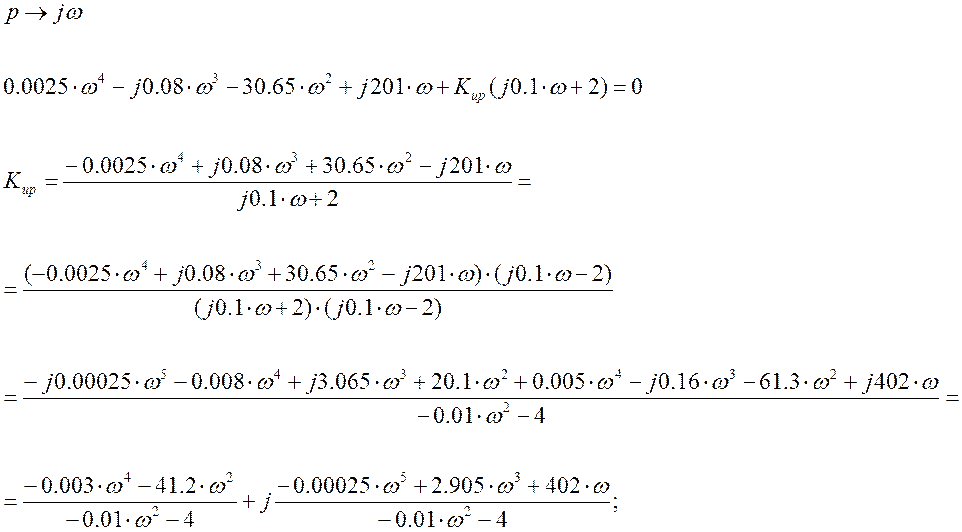
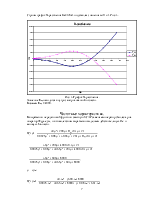
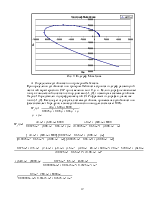
Строим график D-разбиения Re=f(Im), подставляя значения w(0¸¥). Рис. 4.

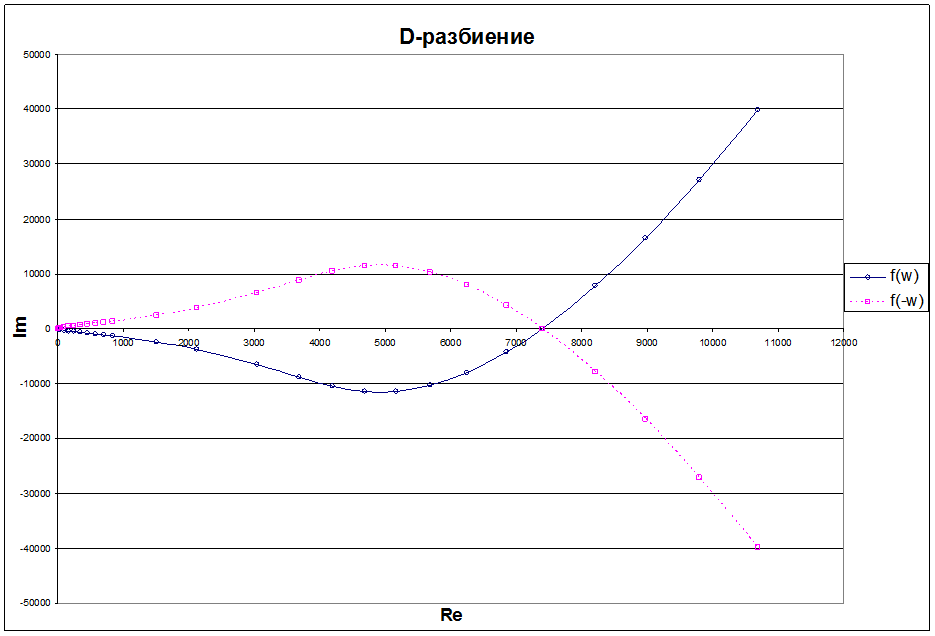
Рис. 4. График D-разбиения.

Значение К_ир находится внутри заштрихованной области.

Возьмем К_ир = 4000.

Частотные характеристики.

В выражении передаточной функции замкнутой САР заменяем оператор Лапласа р на оператор Фурье jw , и в комплексном выражении выделяем действительную Rе   и мнимую  Im части.

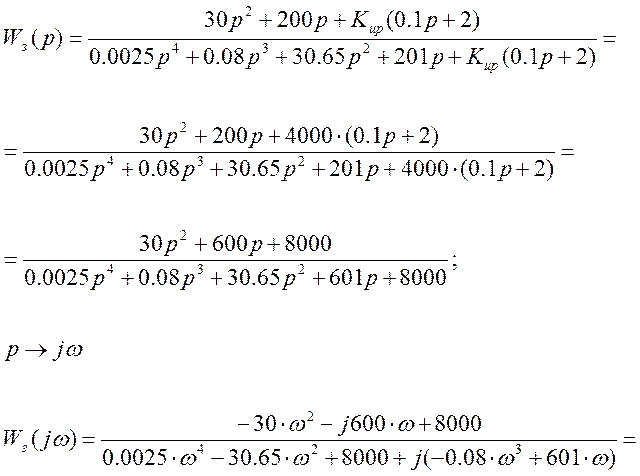
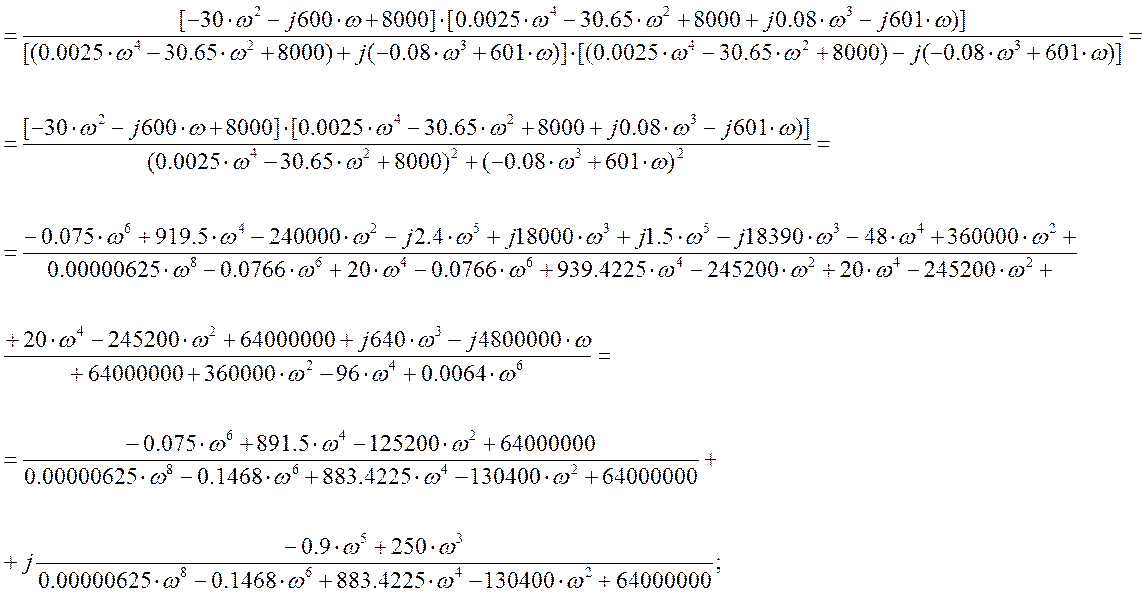
1)  Построение комплексной частотной характеристики (годографа).

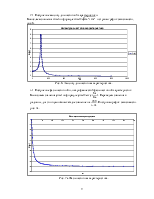
Задаемся w(0¸¥), подставляя в значения реальной Re и мнимой Im частей, строим график Re=f(Im), рис. 5.

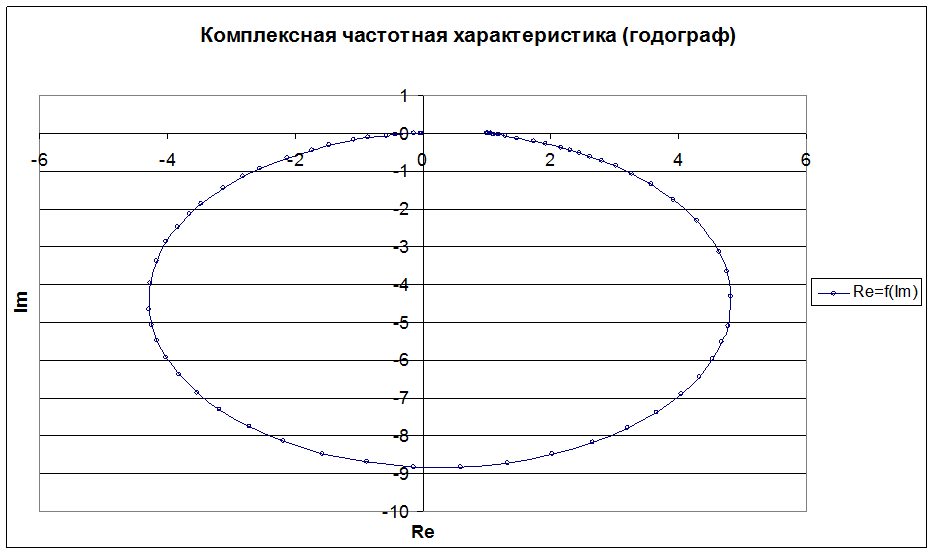
Рис. 5. Комплексная частотная характеристика (годограф).

2)  Построение амплитудно-частотной характеристики.

Вычисляем значения A(w) по формуле A(w)= и строим график зависимости, рис. 6.

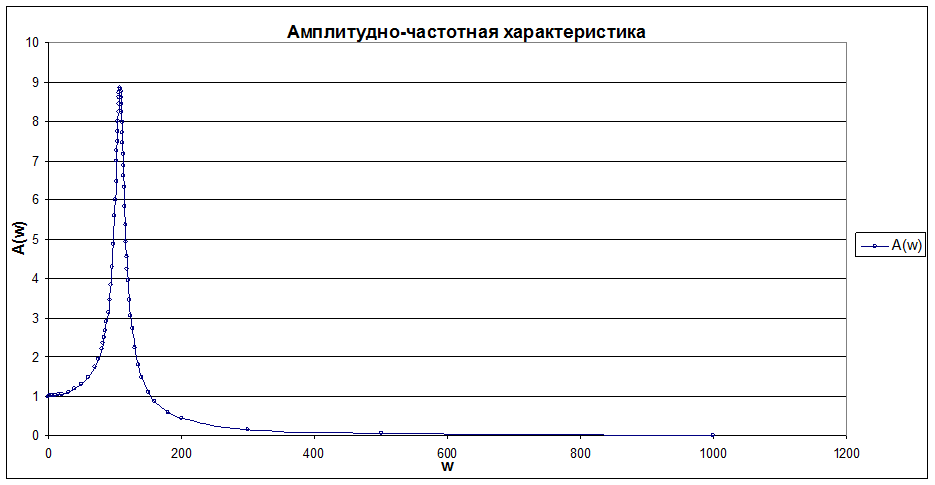
Рис. 6. Амплитудно-частотная характеристика.

3)  Построение фазо-частотной и логарифмической фазо-частотной характеристик.

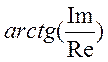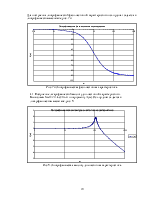
Вычисляем значения j(w) по формуле j (w)=. Переведем значения в радианы, для этого умножим каждое значение на 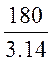. Построим график зависимости, рис. 7а.

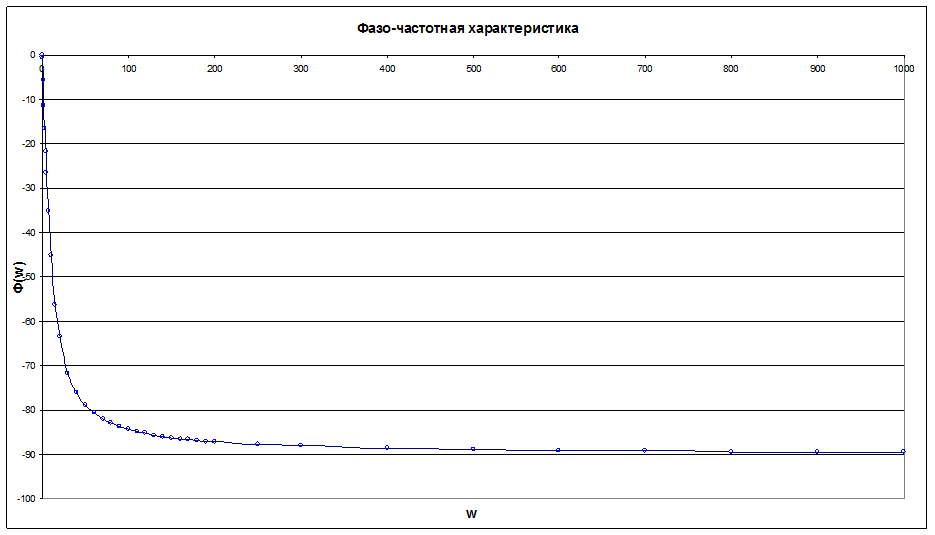
Рис. 7а. Фазо-частотная характеристика.

Для построения логарифмической фазо-частотной характеристики ось ординат задается в логарифмическом масштабе, рис. 7б.

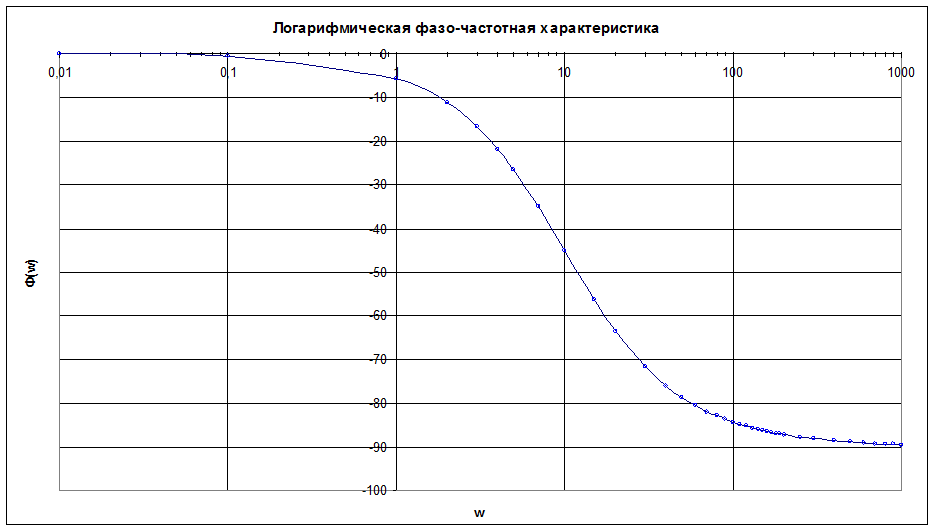
Рис. 7б. Логарифмическая фазо-частотная характеристика.

4)  Построение логарифмической амплитудно-частотной характеристики.

Вычисляем L(w)= по аргументу А(w). Ось ординат задается в логарифмическом масштабе, рис. 8.

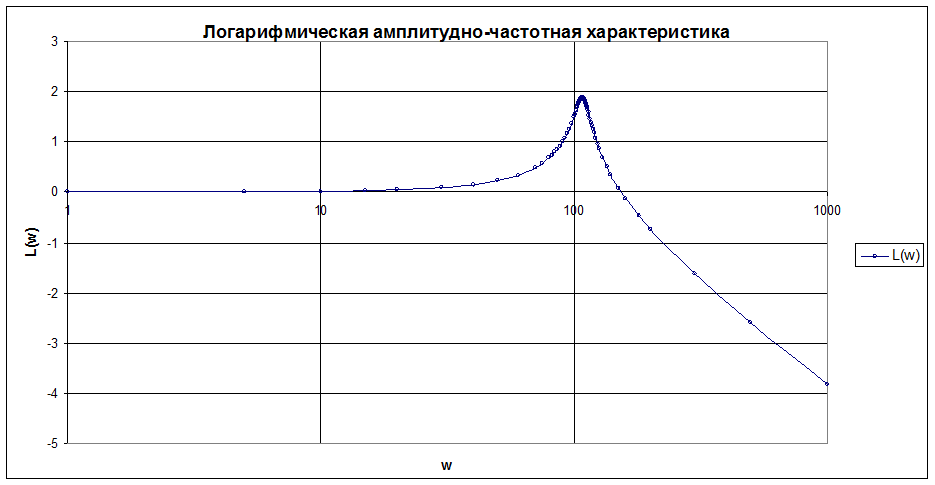
Рис. 8. Логарифмическая амплитудно-частотная характеристика.

Устойчивость САР.

1)  Определение устойчивости по критерию Гурвица.

При определении устойчивости по критерию Гурвица (алгебраический критерий) составляется матрица из коэффициентов характеристического уравнения замкнутой САР.

    a₀               a₁            a₂             a₃          a₄

 

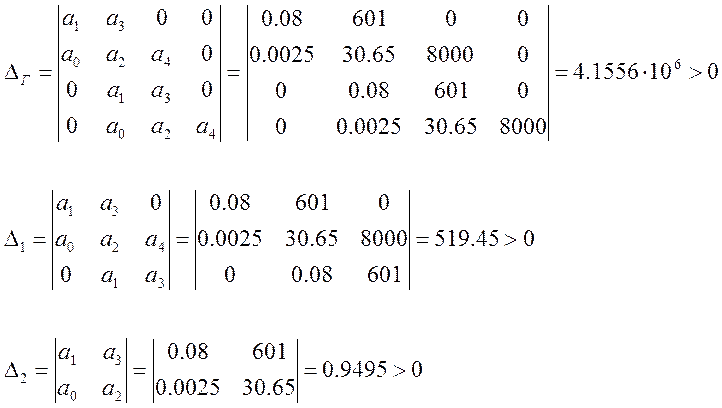
Определитель Гурвица и все его диагональные миноры > 0, это необходимое и достаточное условие, для того чтобы замкнутая САР была устойчива.

2)  Определение устойчивости по критерию Михайлова.

При определении устойчивости по критерию Михайлова анализируется характеристическое уравнение замкнутой САР. Система будет устойчива, если годограф характеристического уравнения замкнутой САР при изменении w от 0 до ∞ пересекает n квадрантов комплексной плоскости, где n – порядок характеристического уравнения, нигде не пересекаясь и не обращаясь в ноль.

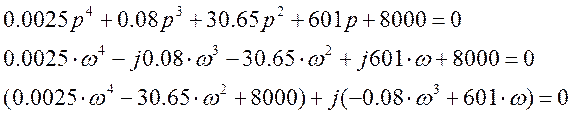
Задаемся w(0¸¥), подставляя в значения реальной Re и мнимой Im частей, строим график Re=f(Im), рис. 9.

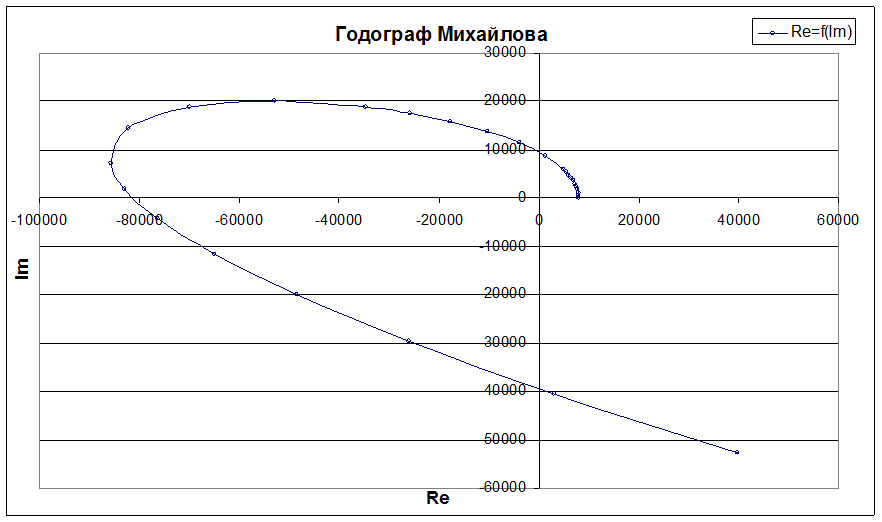
Рис. 9. Годограф Михайлова

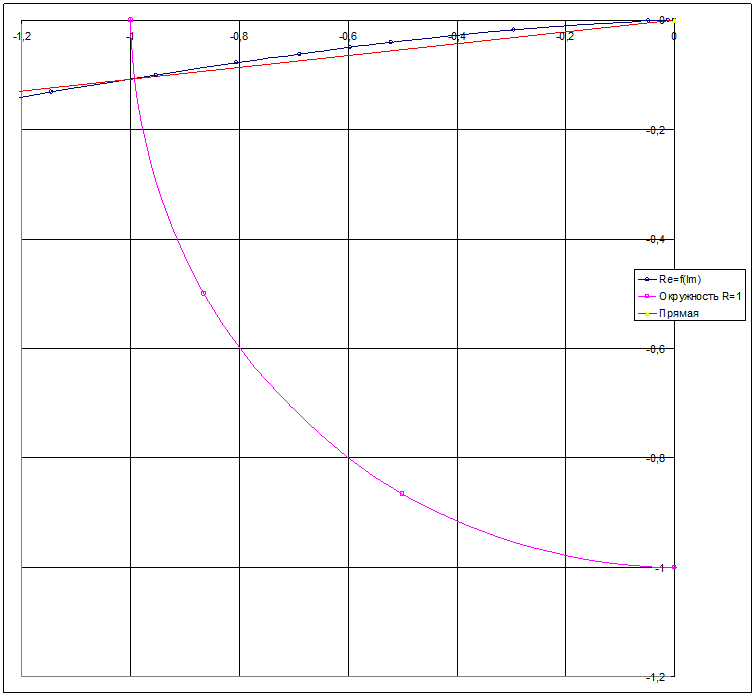
3)  Определение устойчивости по критерию Найквиста.

При определении устойчивости по критерию Найквиста строится годограф разомкнутой частотной характеристики САР при изменении w от 0 до  ∞. Если годограф не охватывает точку в комплексной плоскости с координатами [-1, j0], то замкнутая система устойчива.

На рис. 10 представлен годограф разомкнутой САР и фрагмент годографа в диапазоне точки [-1, j0]. Как следует из рисунка, система устойчива, причем запас устойчивости по фазе составляет 6 градусов, а запас устойчивости по модулю составляет 100%

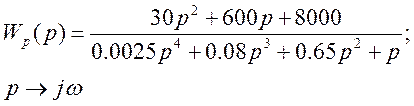
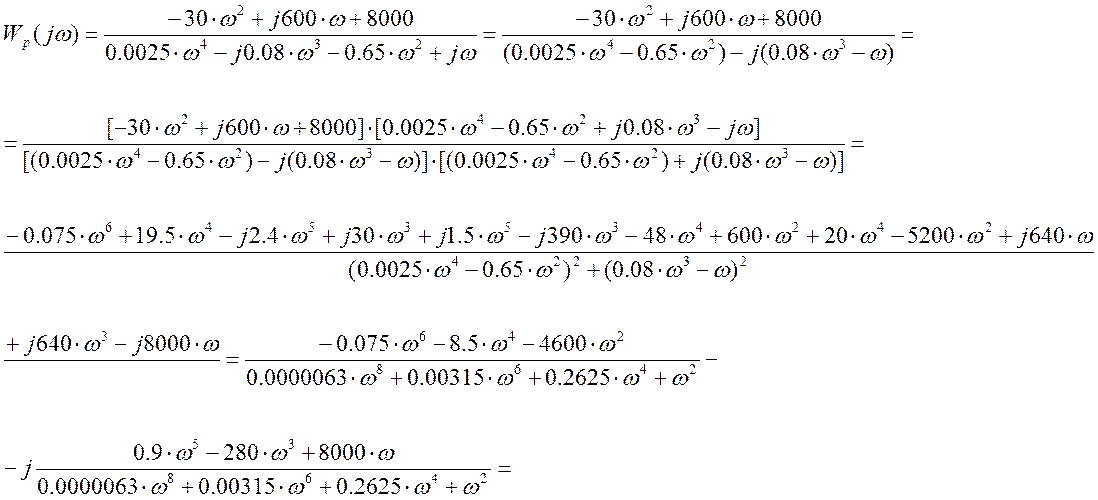
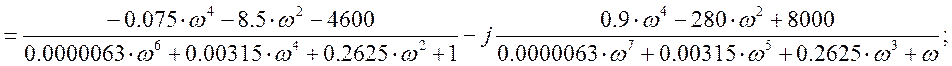
Задаемся w(0¸¥), подставляя в значения реальной Re и мнимой Im частей, строим график Re=f(Im):

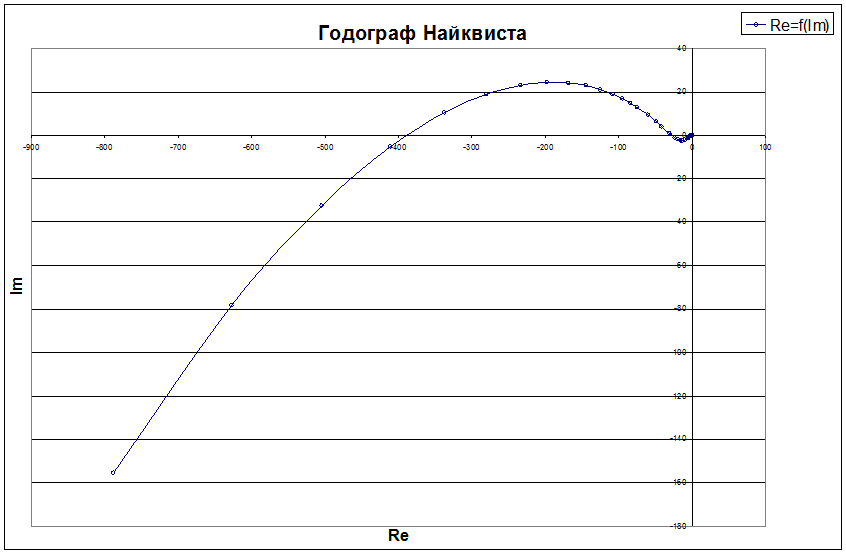
Рис. 10. Годограф Найквиста.

MATLAB-модель САР.

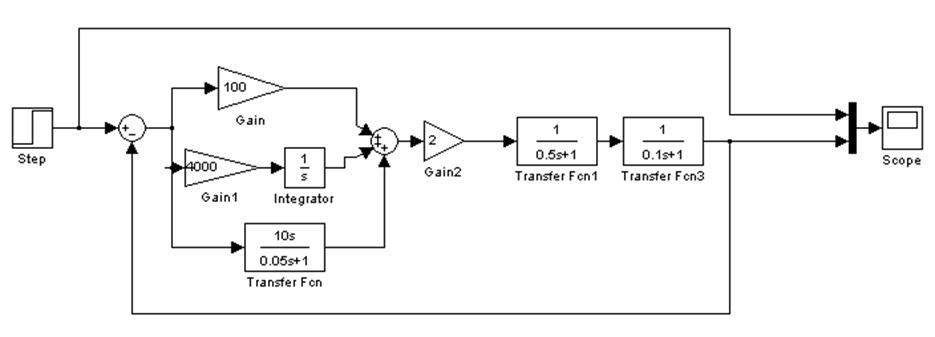
Рис. 11. Схема соединений.

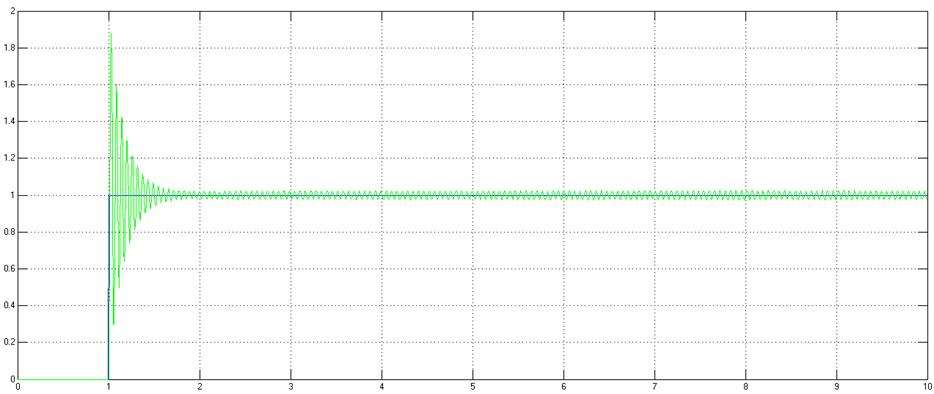
Рис. 12. График. Влияние единичного ступенчатого сигнала на САР.

Система устойчива.