для которого корень |Х|= 1,087. Поэтому она преобразует входной белый шум в нестационарный выход, моделирующий процесс расширенного воспроизводства с темпом, равным 8,7 %.
В практике анализа временных рядов, содержащих нестационарные и периодн- п ческие составляющие, часто прибегают к аппроксимации рядов с помощью надлежащим образом выбранных функций. Эта процедура, называемая обычно выравниванием ряда, не сопряжена с выявлением высокочастотных флуктуации, обусловленных множеством ненаблюдаемых факторов, и дает аналитическое представление регулярных компонент удобное, в частности, для целей их прогнозирования.
Выбранная из тех или иных априорных соображений пробная модель подлежит статистическому оцениванию и диагностической проверке. Для стационарных стохастических моделей процедура оценивания осуществляется методом максимального правдоподобия, рассматриваемым в курсах математической статистики. Среди различных способов диагностики оцененной модели наиболее широкое практическое применение получил корреляционный анализ остатков (остаточных ошибок) е(т), вычисляемых для принятой стационарной модели по данным временного ряда.
Фундаментальной проблемой анализа является построение многофакторных моделей, т.е. выявление причинно-следственных
94
одномерных рядов часто изучается динамика показателя совокупною общественного продукта или национального дохода, валовой продукции отрасли, экономического района, показателей производительности труда, норм материалоемкости, фондоемкости, капиталоемкости, некоторых синтетических показателей уровня жизни и потребления и т. д. При этом принимают, что соответствующий временной ряд порожден многими экзогенными факторами, совместное действие которых моделируют с помощью случайного входа. В одномерной модели идентификации он реализуется в виде последовательности случайных чисел, некоррелированных, со средним, равным нулю, и постоянной конечной дисперсией. Такую последовательность называют дискретным белым шумом. Указанное ^ предположение означает, что структура наблюдаемого ряда обусловлена динамическими свойствами самого объекта.
Дискретные значения входной и выходной последовательностей будем обозначать через Х(х) и У (т) соответственно, а их выборочные значения (ординаты входного и выходного рядов) — через х(г) и (/(т). Входнойбелый шум обозначим через Е (т).
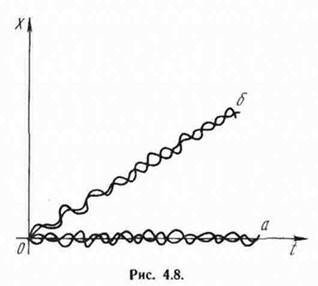
«Внешнее» представление о характере случайного процесса можно получить, рассматривая его реализации Xi(t), х^(1}, ...l Такие пучки, приведенные на рис. 4.8, показывают, что случайные процессы, соответствующие этим реализациям, обладают существенно различными свойствами. Семейство (а) позволяет предполагать, что случайная функция в определенном смысле устойчива во времени, а пучок (б) такой устойчивостью не обладает.
При анализе рядов экономической динамики большей частью пользуются двумя временными характеристиками: средним значением и автокорреляционной (корреляционной) функцией последовательности.
Для динамической идентификации одномерного временного ряда в качестве дискретной модели служит стохастическое
1 В целях наглядности приводятся реализация непрерывного процесса. 95
3, конечно-разностное уравнение, чаще псего линейное с постоянными коэффициентами вида:
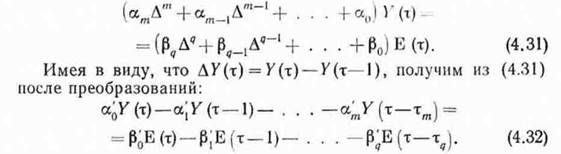
Имея в виду, что АУ(г)=У(т)—У(т—1), получим из (4.31) после преобразований:
,У(т)-а;У(т-1)- . . . -<У(т-т„)= ^Е(т)-Р;Е[т-1)- . . . ~-p;E(T—tJ. (4.32)
а,
Если предполагается, что наблюденный ряд (/=(/(т) стационарен. то для его идентификации выбирается модель вида
(4.32), порождающая стационарный выход У (т), в статистическом отношении адекватный наблюденному ряду (/(т). При входном белом шуме (или в более общем случае—стационарном входе) это условие будет выполнено, если все корни характеристического уравнения для (4.32) будут по абсолютной величине меньше единицы, т. с. |?.|<1. Если хотя бы один из корней больше единицы, то модель неустойчива и при указанном выше входе порождает нестационарную выходную последовательность (см. 4.1.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.