Рассмотрим далее понятия условной и безусловной оптимизации.
В задачах безусловной оптимизации отсутствуют какие либо ограничения на возможные значения переменных оптимизации xj (j=1,2, ... , n).
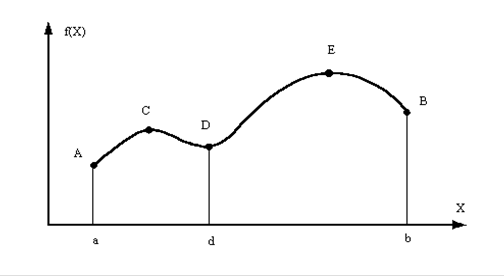 |
Рис.1.1
.
Задачами условной оптимизации называют такие задачи, в которых помимо целевой функции задаются некоторые дополнительные условия, которые должны быть выполнены. Эти условия задаются в виде некоторых ограничений на множество возможных значений переменных xi .
Введение ограничений либо не влияет на оптимум, либо ухудшает его. Например, если для целевой функции, приведенной на рисунке 1.1, задать ограничение x £ d , то максимум будет достигаться в точке C. При этом произойдет ухудшение значения максимума, достигаемого при отсутствии ограничений в точке E.
Оптимум, как и экстремум, может быть как локальным, так и глобальным. Необходимость во введении таких понятий возникает при наличии нескольких одноименных оптимумов (в том числе и экстремумов) на некотором ограниченном множестве значений X. Например, в случае, приводимом на рисунке 1.1, функция f(x) принимает минимальные значения на отрезке [a, b] в трех точках: A, D и B. При этом глобальный оптимум (в данном случае минимум) будет достигаться в граничной точке А.
Отметим часто используемые в дальнейшем связи между задачами максимизации и минимизации одной и той же целевой функции:
max z = - min(-z) , min z = - max(-z) , (1.2)
где maxz и minz – максимум и минимум функции z, достигаемые в некоторой точке экстремума (оптимума).
Справедливость таких соотношений иллюстрируется рисунком 1.2.
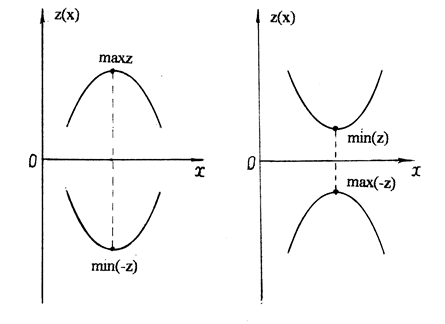
Рис. 1.2
Соотношения (1.2) позволяют формально сводить задачу оптимизации, требующую поиска одного вида оптимума, к задаче, требующей поиска другого вида оптимума.
Рассмотрим далее последовательность решения задачи оптимизации. Такая последовательность обычно разбивается на несколько этапов. Будем в дальнейшем выделять следующие основные этапы решения задачи оптимизации:
1) содержательная постановка задачи;
2) построение математической модели задачи оптимизации (математическая постановка задачи);
3) поиск решения;
4) содержательная интерпретация результатов решения задачи.
На первом этапе производится словесная формулировка задачи оптимального выбора. Она не должна содержать избыточной информации и в то же время содержать всю необходимую информацию, описывающую условия задачи. Из такой формулировки должна следовать возможность нескольких (как минимум, двух) вариантов решения задачи. Из нее должно быть также ясным, в каком смысле искомое решение должно быть наилучшим и какая величина может быть принята в качестве критерия оптимизации. Из этой формулировки должен быть ясен также характер зависимостей между переменными задачи и характер ограничений на эти переменные.
Содержательная постановка задачи производится в терминах той предметной области, в которой требуется решить задачу оптимизации. В рамках изучаемого нами курса содержательная постановка задачи оптимизации является постановкой задачи оптимального проектирования.
На втором этапе с помощью специальной математической символики производится формализация содержательной постановка задачи. При этом формально описываются цель оптимизации, аргументы и структура целевой функции, а также области допустимых изменений ее аргументов. Такая запись обычно называется математической моделью задачи оптимизации (реже - математической постановкой задачи).
На третьем этапе осуществляется выбор наилучшего варианта из множества возможных вариантов. Такой выбор осуществляется в соответствии с некоторым методом оптимизации. В большинстве случаев такой метод имеет форму алгоритма, реализуемого на ЭВМ
На четвертом этапе результат решения задачи оптимизации, полученный в математической символике, “переводится” на содержательный язык предметной области.
1.2. Общая характеристика методов оптимизации
Дадим далее общую характеристику методов оптимизации, составляющих основное содержание настоящего курса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.