Линейное программирование. Геометрическая интерпретация и графический метод решения задачи линейного программирования, страница 11

В этой таблице над обозначениями векторов A₁, A₂, …, A_n проставлены коэффициенты целевой функции задачи. В процессе решения в столбце X_B находится список базисных переменных, а в столбце C_B – соответствующие им коэффициенты целевой функции. В столбце B находятся коэффициенты системы ограничений, соответствующие базисным переменным, в столбцах A₁, A₂, …, A_n – коэффициенты a_ij матрицы условий, в оценочной (индексной) строке D – значение целевой функции z₀ и оценки переменных оптимизации D_j .

При заполнении элементов D-строки исходной таблицы используются формулы (2.17), (2.18), а также формула

                             z₀  = c_ib_i  ,                                            (2.24)

в которой индексом i нумеруются базисные переменные ( iÌ I_B ).

Опишем алгоритм симплекс-метода (для случая максимизации).

1. Находим начальный опорный план. Он имеет вид (2.16).

2. Рассчитываем значения оценок D_jпо формулам (2.17) и (2.18), а также значение целевой функции z₀.

Определяем знаки оценок. Если все D_j³ 0, то задача решена: опорный план оптимален, max z  = z₀.

Если исходная задача имела стандартную форму, то переходим к ее оптимальному плану, удаляя из полученного плана значения дополнительных переменных.

Если не все D_j³ 0, переходим к шагу 3.

3. Среди значений D_j < 0 находим наибольшее по абсолютной величине, и соответствующий ему столбец выбираем в качестве ведущего.  Пусть это будет столбец с номером s. Если в ведущем столбце элементы a_is £ 0 для всех i=1, …, m , то целевая функция не ограничена, max z =¥. Решение окончено.

Если не все a_is £ 0, то переходим к шагу 4.

4. Для каждого элемента a_is > 0 ведущего столбца находим отношение b_i / a_is , выбираем наименьшее из них и называем строку, где оно достигается, ведущей.  Пусть это будет строка с номером r. Элемент a_rs на пересечении ведущего столбца и ведущей строки будет ведущим.

5. Выполняем жорданово преобразование таблицы с ведущим элементом a_rs по формулам (2.14), (2.15) и переходим к шагу 2.

Последовательность операций 2 … 5 называется итерацией симплекс-метода.

З а м е ч а н и е 2.18. При нумерации элементов матрицы A и столбца B в пунктах. 3, 4 и 5 в качестве индекса i будем использовать не обычный  номер строки, а номер базисной переменной.

З а м е ч а н и е 2.19. После выполнения преобразований на шаге 5 в симплекс-таблице в столбце X_B необходимо заменить одну из базисных переменных (переменную с номером s на переменную с номером r ). Соответственно должен измениться и набор значений коэффициентов в столбцах B  и  C_B.

З а м е ч а н и е 2.20. При реализации симплекс-метода результаты выполнения каждой итерации показываются в симплекс-таблицах. Такие таблицы выполняются на момент окончания расчета оценок на этапе 2.

Замечание 2.21. При решении M-задачи из симплекс-таблиц можно последовательно исключать столбцы, соответствующие переменным, выведенным из базиса.

Замечание 2.22. Дополнительным признаком окончания итераций в M-задаче (при ограниченности ЦФ) является равенство нулю всех искусственных переменных. 

Рассмотрим простейший пример, иллюстрирующий использование симплекс-метода и его геометрическую трактовку.

Пусть задача ЛП имеет вид :

z = 2x₁ + x₂ ® max

2x₁ + 3x₂ £ 6

x₁ ³ 0 , x₂ ³ 0 .

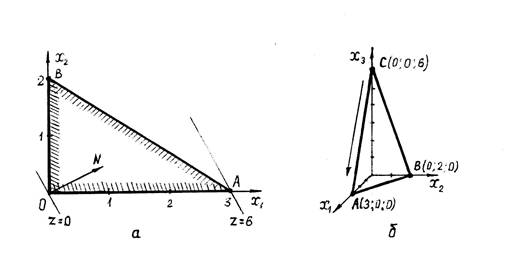
Решим эту задачу сначала геометрическим методом. Такое решение иллюстрируется рисунком 2.5.а.

Решение этой задачи имеет вид: X_опт = (3 ; 0) , z_опт = 6.

Для решения этой задачи симплекс-методом переведем ее в каноРис. 2.5

ническую форму (построим расширенную задачу). Для этого введем дополнительную переменную x₃ . Получим уравнение (играющее роль системы уравнений) вида

2x₁ + 3x₂  + x₃ = 6 .

Составим первую симплекс-таблицу (таблица 2.2). Из этой таблицы следует, что начальный опорный план имеет вид

X = ( 0 ; 0 ; 6 )