Линейное программирование. Геометрическая интерпретация и графический метод решения задачи линейного программирования

2.  Линейное программирование

          2.1.  Общая характеристика задачи

Линейное программирование (ЛП) – это область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейными зависимостями в целевой функции и ограничениях. (Понятие линейной функции было дано  в замечании 1.8)

Особенно широкое применение ЛП нашло в экономике и организации производства. Многочисленные примеры экономических и организационных задач, сводимых к задаче ЛП, приведены в [4…8]. Применение ЛП при решении задач оптимального проектирования   ограниченно. Вместе с тем методы решения задач ЛП иллюстрируют общие принципы решения задач МП и являются основой ряда других методов МП, применяемых в САПР.

          2.2.  Постановки задач линейного программирования

Постановки задач ЛП имеют различные формы. В одних задачах целевая функция должна быть максимизирована, в других – минимизирована. Ограничения на переменные могут быть заданы равенствами или неравенствами. Кроме того, в некоторых задачах требование неотрицательности может распространяться не на все переменные.

З а м е ч а н и е 2.1. В дальнейшем для определенности все теоретические положения ЛП будут сформулированы  для задачи максимизации. Тем не менее, на основе использования соотношений (1.2) они могут быть перенесены и на задачу минимизации.

В зависимости от особенностей системы ограничений все постановки задачи ЛП  укладываются в три основные формы: стандартную, каноническую и  общую.

 Стандартная  задача  ЛП имеет вид:

max z = c₁x₁+c₂x₂+…+c_nx_{n  ,}

                            a₁₁x₁+a₁₂x₂+…+a_1nx_n  £ b_{1 ,}

                           a₂₁x₁+a₂₂x₂+…+a_2nx_n  £ b_{2 ,}

.   .   .   .   .   .   .                                          (2.1)  

                            a_m1x₁+a_m2x₂+…+a_mnx_n  £ b_{m  ,}

                            x₁ ³0, x₂ ³0, …, x_n ³ 0.

Это задача с однотипными ограничениями-неравенствами и неотрицательными переменными.

Введя обозначения

C=(c₁, c₂, …, c_n);

A =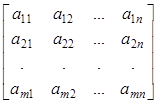;      X =  ;     B = , можем записать стандартную задачу в  матричной форме:

max z=CX;  AX£B;  X³0.                                         (2.2)

Здесь линейная зависимость (форма) c₁x₁+c₂x₂+…+c_nx_n записана в виде скалярного произведения CX  векторов C и X.

З а м е ч а н и е 2.2. В дальнейшем вектор X, использующийся в матричных формах записи задач ЛП в виде вектора-столбца, в тексте будем использовать в форме вектора-строки X^т =(x₁, x₂, …,x_n ) . При этом символ транспонирования “т” будем опускать.

Введем для j-го столбца матрицы A обозначение A_j. Тогда получим еще одну – векторную форму записи этой задачи

max z = c₁x₁+c₂x₂+…+c_nx_{n  ,}

                 A₁x₁+A₂x₂+…+A_nx_n £ B ,                                        (2.3)

                  x₁ ³0, x₂ ³0, …, x_n ³0.

З а м е ч а н и е 2.3. Во второй строке постановки (2.3) каждое из слагаемых в левой части неравенства представляет собой вектор, являющийся произведением вектора-столбца на число.

В стандартной задаче соотношение между числом неизвестных n и числом ограничений m может быть произвольным: задача имеет смысл при n >m, n =m, n <m.

Канонической задачей  называется задача ЛП, в которой все переменные неотрицательны и ограничения имеют форму равенств :

                  max z = CX ;   AX = B ;   X ³ 0.(2.4)

В канонической задаче число неизвестных всегда больше числа уравнений (n>m). Это обусловлено тем, что, если число неизвестных равно числу уравнений и уравнения линейно независимы, то система имеет единственное решение. Очевидно, что в этом случае в связи с отсутствием выбора задача оптимизации не возникает.

З а м е ч а н и е 2.4. Будем в дальнейшем считать, что среди уравнений системы ограничений канонической задачи нет «лишних», т.е. что они образуют систему линейных независимых уравнений, и матрица условий задачи имеет ранг m.

Каноническая задача  также может быть представлена в векторной форме, аналогичной (2.3).

Каноническая задача имеет ряд разновидностей. Так в [16] рассматривается допустимая каноническая форма задачи ЛП. В такой форме b_j ³  0. 

Важным частным случаем канонической задачи является каноническая задача в базисной форме, отличающаяся тем, что все коэффициенты вектора ограничений Bнеотрицательны,  b_i ³ 0 (i=1, …, m) и в каждом уравнении имеется переменная с коэффициентом 1, которая не входит ни в одно из остальных уравнений.

Система ограничений такой задачи имеет вид:

                  x_i   +a_ij x_j = b_i,     i =1, …, m .(2.5)

Переменные x_i  в этом выражении, обладающие указанным свойством, называются  базисными.

Общей задачей линейного программирования называется задача, в которой имеются ограничения как в виде равенств, так и неравенств. Кроме того, требование неотрицательности может быть наложено не на все переменные.

З а м е ч а н и е 2.5. Отметим отсутствие единообразия в названиях форм постановок общей задачи ЛП. Так, в [7, 8] базисную форму (2.5) называют канонической, а каноническую форму (2.4)  стандартной.