Числовые ряды. Сходимость числового ряда, страница 4

В пункте  8.1.1  мы  выяснили,  что 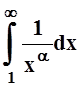   сходится  тогда  и только тогда, когда a> 1 (советуем читателю выполнить сейчас это простое вычисление интеграла ). Поэтому можно сделать вывод:

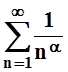   сходится        Ûa> 1.

Обобщённые гармонические ряды удобно использовать для исследования сходимости различных числовых рядов с помощью признаков сравнения (см. примеры ниже, в разделе 13.5).

Приведём ещё один пример использования интегрального признака.

Пример 10.  Исследовать сходимость ряда   .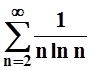

Решение. Рассмотрим функцию  .  При x ³ 2 она удовлетворяет условиям теоремы 9, поэтому ряд  и интеграл  или оба сходятся, или оба расходятся.  Вычислим интеграл:

.

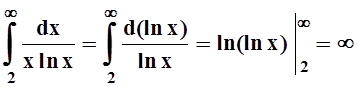(Напомним: эта короткая запись фактически означает, что ). Интеграл расходится, значит, расходится и ряд.

Обратим внимание читателя на одно любопытное обстоятельство. Гармонический ряд  является в определённом смысле пограничным: он расходится, но стоит лишь хотя бы немного увеличить показатель (например, рассмотреть ряд ) и ряд будет сходиться.  С другой стороны ,  – бесконечно малая более высокого порядка, чем , однако ряд  расходится. Более того, можно построить целую серию рядов

 .

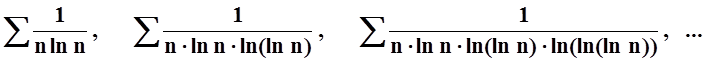Все эти ряды расходятся – это легко проверить с помощью интегрального признака. Однако общий член a_n каждого последующего ряда стремится к 0 быстрее, чем у предыдущего ряда.

13.3   Знакопеременные ряды

Теперь будем рассматривать числовые ряды, члены которых могут быть как положительными, так и отрицательными числами. Наиболее простой и важный случай – ряды, у которых знаки соседних слагаемых противоположны. Такие ряды называются знакочередующимися. Будем записывать знакочередующиеся ряды так:

.

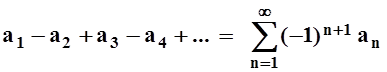Здесь числа  a_n  предполагаются положительными:  a_n ³ 0.

Для знакочередующихся рядов основной является

Теорема 10 (теорема Лейбница). Пусть для знакочередующегося ряда  выполнены условия:

1)   ,                  2)   .

Тогда ряд сходится, причём его сумма не больше, чем первое слагаемое   a₁.

Доказательство. Рассмотрим частичные суммы с чётными номерами. Можно записать:

.

Из условия теоремы следует, что все скобки здесь положительны. Поэтому последовательность {S_2k} возрастающая. Можно  S_2k записать по–другому:

S_2k = a₁ – (a₂ – a₃) – (a₄ – a₅) –...– (a_2k–2 – a_2k–1) – a_2k.

Так как из числа а₁ вычитаются положительные числа, то получаем: S_2k £ a₁. В частности, последовательность {S_2k} ограничена сверху. Возрастающая, ограниченная сверху последовательность имеет предел (1.4.2):

.

Так как  S_2k £ a₁   при любом   k,   то и   S £ a₁ .

Заметим теперь, что частичные суммы с нечётными номерами тоже стремятся к S:

S_2k+1 = S_2k + a_2k+1,      lim S_2k+1 = lim S_2k + lim a_2k+1 = S + 0 = S.

(Мы используем условие теоремы:  ). Теперь ясно, что число S является пределом всей последовательности {S_n}: в любой окрестности  S  находятся как чётные, так и нечётные (т.е. любые) частичные суммы с достаточно большими номерами. Теорема доказана.

Пример 11.  Исследовать сходимость ряда

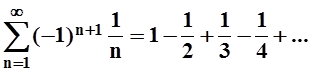
Решение.Ряд знакочередующийся, условия теоремы Лейбница, очевидно, выполнены. Значит, ряд сходится. В дальнейшем мы выясним, что его сумма равна ln2.

Замечание. Требование монотонности убывания а_n в теореме Лейбница является существенным. Одного лишь условия lim a_n = 0 недостаточно для сходимости даже знакочередующегося ряда. Рассмотрим, например, знакочередующийся ряд

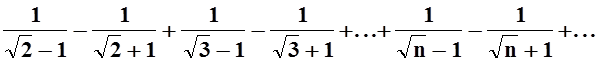
Требование lim a_n = 0, очевидно, выполнено. Вычислим сумму первых  2n слагаемых:

.

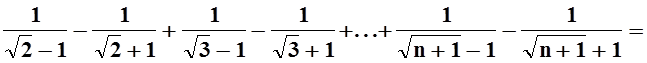
Как мы уже знаем, такая сумма стремится к бесконечности (при n®¥), так как это частичная сумма ряда  .  Следовательно, ряд расходится.

Дальше