13 Числовые ряды
Мы начинаем изучать новую тему – теорию рядов. Понятие ряда обобщает понятие суммы, позволяя рассматривать суммы бесконечного числа слагаемых. Основа для такого обобщения у нас есть – это теория числовых последовательностей, рассмотренная в 1 модуле.
13.1 Сходимость числового ряда
Пусть a1, a2, a3, ..., ak,... – действительные числа. Числовым рядом называется выражение
a1 + a2 + a3 + ... + ak + ...
Можно записывать ряд и с помощью значка S:
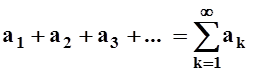 .
.
Нумерацию слагаемых иногда начинают не с 1, а с 0 (или другого целого числа). Таким образом, числовой ряд – совершенно новый для нас объект. Пока – это лишь символическая запись указанного вида, содержательный смысл этой записи нам предстоит определить. Рассмотрим числа:
S1 = a1,
S2 = a1 + a2,
S3 = a1 + a2 + a3,
……………………
Sn = a1 + a2 + ... + an,
………………………
Они называются частичными суммамиряда
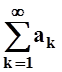 . Если последовательность {Sn} сходится, т.е. существует
конечный предел
. Если последовательность {Sn} сходится, т.е. существует
конечный предел ![]() , то ряд
, то ряд 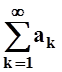 называется сходящимся,
а число S – суммой этого
ряда. Если lim Sn
бесконечен или не существует, то ряд называется расходящимся.
называется сходящимся,
а число S – суммой этого
ряда. Если lim Sn
бесконечен или не существует, то ряд называется расходящимся.
Пример
1. Ряд 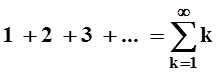 расходится, так как
последовательность его частичных сумм, очевидно, стремится к бесконечности.
расходится, так как
последовательность его частичных сумм, очевидно, стремится к бесконечности.
Ряд 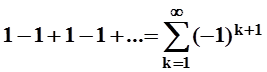 тоже расходится, его частичные
суммы S1 = 1, S2 = 0, S3 = 1, S4 = 0, ... образуют последовательность, не
имеющую предела.
тоже расходится, его частичные
суммы S1 = 1, S2 = 0, S3 = 1, S4 = 0, ... образуют последовательность, не
имеющую предела.
Пример 2. Рассмотрим ряд
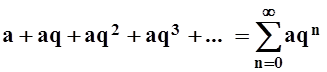 .
.
Он представляет собой сумму геометрической прогрессии. Напомним: а – первый член, q – знаменатель прогрессии. Попытаемся разобраться: сходится ли этот ряд?
Рассмотрим частичную сумму: Sn = a + aq +...+ aqn–1. Умножим обе части равенства на q, а затем вычтем одно равенство из другого:
Snq = aq + aq2 + ... + aqn,
Sn – Snq = a – aqn.
Отсюда находим: 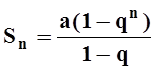 . Впрочем, эта формула для суммы
первых n членов геометрической
прогрессии рассматривается в школьном курсе математики. Вычислим предел:
. Впрочем, эта формула для суммы
первых n членов геометрической
прогрессии рассматривается в школьном курсе математики. Вычислим предел:
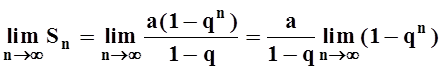
Как мы знаем, если ![]() , то
, то ![]() (при
(при
![]() ). Поэтому при
). Поэтому при ![]() ряд сходится:
ряд сходится:
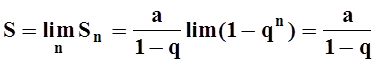
– сумма бесконечной убывающей
геометрической прогрессии. Если же ![]() , то
, то ![]() и ряд расходится. Итак,
запомним:
и ряд расходится. Итак,
запомним:
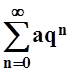 сходится
сходится ![]() .
.
Пример 3. Рассмотрим ряд
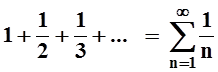 .
.
Этот так называемый гармонический ряд. Чтобы решить вопрос о его сходимости, рассмотрим другой, вспомогательный ряд, полученный из гармонического уменьшением его слагаемых:
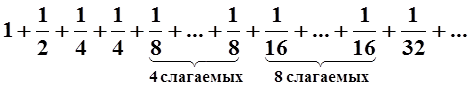
( Мы в гармоническом ряде
оставили слагаемые ![]() без изменения, а остальные
уменьшили). Подсчитаем некоторые частичные суммы нового ряда:
без изменения, а остальные
уменьшили). Подсчитаем некоторые частичные суммы нового ряда:
![]()
![]() .
.
Ясно, что ![]() . Значит,
. Значит, ![]() . Поэтому вспомогательный ряд
расходится (последовательность Sn
не может сходиться, если некоторая её подпоследовательность стремится к ¥). Частичные суммы
гармонического ряда больше соответствующих Sn,
поэтому гармонический ряд расходится.
. Поэтому вспомогательный ряд
расходится (последовательность Sn
не может сходиться, если некоторая её подпоследовательность стремится к ¥). Частичные суммы
гармонического ряда больше соответствующих Sn,
поэтому гармонический ряд расходится.
Перейдём к изучению свойств сходящихся рядов.
Теорема
1. Рассмотрим ряд 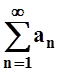 , а также ряд,
полученный из него отбрасыванием первых k
слагаемых:
, а также ряд,
полученный из него отбрасыванием первых k
слагаемых: 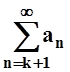 . Эти ряды или оба сходятся, или оба
расходятся.
. Эти ряды или оба сходятся, или оба
расходятся.
Доказательство.
Обозначим Sn –
частичные суммы ряда 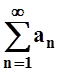 , S¢n
– частичные суммы ряда
, S¢n
– частичные суммы ряда 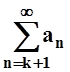 . Ясно, что
тогда
. Ясно, что
тогда ![]() . Поэтому
. Поэтому ![]() . Но
. Но ![]() ,
а значит если существует и конечен один из пределов
,
а значит если существует и конечен один из пределов ![]() ,
то существует и конечен другой предел, что и требовалось доказать.
,
то существует и конечен другой предел, что и требовалось доказать.
Итак,
сходимость ряда (как и сходимость числовой последовательности) не зависит от
первых членов. Сходимость или расходимость характеризует поведение слагаемых an при n®¥. Изучая сходимость ряда, можно вместо записи 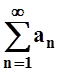 использовать более простую запись
использовать более простую запись ![]() .
.
Теорема
2. Если ряды 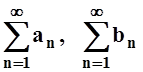 сходятся, то сходятся и
ряды
сходятся, то сходятся и
ряды 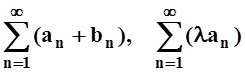 . Здесь l–
действительное число.
. Здесь l–
действительное число.
Доказательство
сразу следует из определения сходящегося ряда и свойств предела
последовательности. Действительно, если Sn, S¢n–
частичные суммы рядов ![]() соответственно, то
соответственно, то ![]() – частичные суммы рядов
– частичные суммы рядов ![]() . Значит, если lim Sn, lim S¢n
существуют и конечны, то существуют и конечны также пределы
. Значит, если lim Sn, lim S¢n
существуют и конечны, то существуют и конечны также пределы
![]() .
.
Теорема
3 (необходимое условие сходимости). Если ряд ![]() сходится, то
сходится, то ![]() .
.
Доказательство.
По определению, сходимость ряда означает, что существует конечный предел ![]() . Но
. Но ![]() .
Поэтому
.
Поэтому
![]() .
.
Замечание.
Условие lim an = 0 не является достаточным
для сходимости ряда – например, для гармонического ряда ![]() оно,
очевидно, выполнено, однако ряд расходится. Таким образом, с помощью теоремы 3
иногда можно убедиться в расходимости ряда, но доказать сходимость нельзя.
оно,
очевидно, выполнено, однако ряд расходится. Таким образом, с помощью теоремы 3
иногда можно убедиться в расходимости ряда, но доказать сходимость нельзя.
Пример
4. Исследовать сходимость ряда ![]()
Решение. Замечая закономерность в изменении слагаемых, можем записать ряд так:
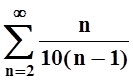 .
.
Другими словами, 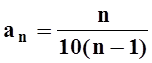 . Вычислим предел:
. Вычислим предел:
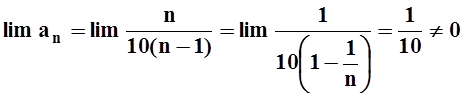 .
.
Ряд расходится, так как нарушено необходимое условие сходимости.
Теорема 4 (критерий Коши сходимости числового ряда).
![]() сходится
сходится 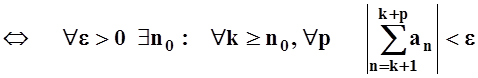 .
.
Доказательство. Пусть {Sn} – последовательность частичных сумм.
Ряд ![]() сходится Û {Sn} сходится Û {Sn} фундаментальна,
т.е.
сходится Û {Sn} сходится Û {Sn} фундаментальна,
т.е.
![]() .Мы
воспользовались критерием Коши для числовых последовательностей (см. 1.4.4).
Записывая последнее утверждение немного в другой форме, получим:
.Мы
воспользовались критерием Коши для числовых последовательностей (см. 1.4.4).
Записывая последнее утверждение немного в другой форме, получим:
![]() , или, что то же самое,
, или, что то же самое,
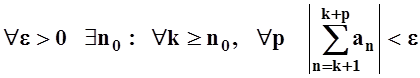 .
.
Заметим, что
не только для каждого ряда ![]() можно
рассмотреть последовательность {Sn},
но и наоборот, зная последовательность частичных сумм, можно найти слагаемые
ряда: an = Sn–Sn–1.
Таким образом, каждому числовому ряду однозначно соответствует
последовательность. Причём сходимость ряда означает сходимость
соответствующей последовательности. Поэтому многие свойства числовых рядов
(например теоремы 1, 3, 4) – это свойства последовательностей, сформулированные
на «языке рядов».
можно
рассмотреть последовательность {Sn},
но и наоборот, зная последовательность частичных сумм, можно найти слагаемые
ряда: an = Sn–Sn–1.
Таким образом, каждому числовому ряду однозначно соответствует
последовательность. Причём сходимость ряда означает сходимость
соответствующей последовательности. Поэтому многие свойства числовых рядов
(например теоремы 1, 3, 4) – это свойства последовательностей, сформулированные
на «языке рядов».
13.2 Признаки сходимости рядов с положительными слагаемыми
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.