Функции нескольких переменных. Множества в n-мерном евклидовом пространстве, страница 4

Используется обычное обозначение:    То же самое можно сказать на «языке окрестностей». Правда, здесь нужна «проколотая» окрестность:

в частности, потому, что в точке  P_o  функция может быть не определена.  Итак,

.

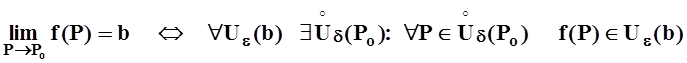Наконец, используя известное нам понятие предела последовательности точек Rⁿ, можно дать определение на «языке последовательностей»:

Часто, рассматривая функции 2–х переменных, точки на плоскости обозначают не одной буквой P, а парой (x,y). Для обозначения предела функции тогда применяются записи:

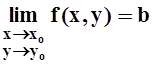            или             .

Замечание.Сравнивая разные способы определения предела функции нескольких переменных с аналогичными определениями для функции одной переменной, мы видим очень много общего. В частности, буквально так же, как в разделе 2.2, можно доказать, что все три подхода равносильны. Как и ранее, из определения предела следует, что его величина не должна зависеть от способа стремления к предельной точке. Однако для случая одной переменной достаточно было рассмотреть 2 способа стремления – слева и справа. Теперь же, даже при  n = 2,  способов приближения к предельной точке бесконечно много. Это создаёт трудности при вычислении пределов.

Пример 2 .  Вычислить   .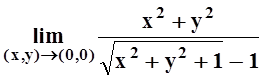

Решение. Независимо от способа (пути) стремления   (x,y)®(0,0),  величина x²+y²  стремится к нулю. Поэтому, обозначая   x²+y² = t,  можно перейти к функции одной переменной.

.

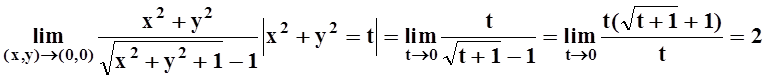Пример 3 .  Вычислить  .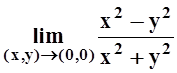

Решение.  Здесь не видно, как перейти к функции одной переменной. Попробуем сначала перейти к пределу при  y ® 0, оставляя  х  без изменения, а затем потребовать, чтобы  x ® 0.

 .

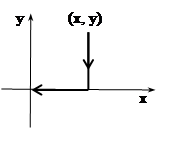
Такой способ вычисления называется повторным пределом. На рисунке указан путь приближения (x,y)®(0,0). Теперь вычислим другой повторный предел, приближаясь к предельной точке по другой ломаной:

.

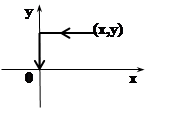
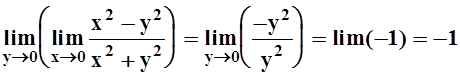Получаем разные результаты, поэтому исходный предел не существует.

Однако даже совпадение повторных пределов ещё не гарантирует существования предела – имеется много других путей приближения к предельной точке, они могут привести к другим результатам.

Пример 4.  Вычислить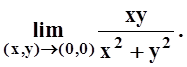 

Решение. Вычислим повторные пределы:

,                  

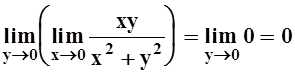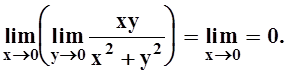
Значит, если предел существует, то он равен 0. Но ведь есть много других способов приближения  (x,y) ® (0,0).   Попробуем двигаться к точке  (0, 0)  по лучу  y = kx:

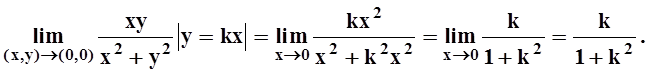
Результат зависит от k, по разным путям получаются разные значения. Следовательно, предел не существует.

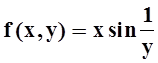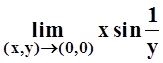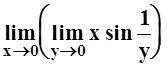Замечание. Операция вычисления повторного предела содержит промежуточный предельный переход, который может оказаться неосуществимым, даже если предел функции существует. Например, для функции  предел  существует и, очевидно, равен 0.Однако повторный предел     не существует, так как при  x ¹ 0   не существует  .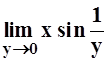

Арифметические свойства пределов функции нескольких переменных не отличаются от случая одной переменной.

Теорема 6.     Если        то

,             ,

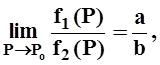           если только  b¹ 0.

Доказательство  проводится с помощью свойств числовых последовательностей, в точности так же, как для функций одной переменной (теорема 5 из 2.2)

9.3   Определение и свойства непрерывных функций

Функция f называется  непрерывной в точке P_o, если она определена в этой точке и

.

Если  P_o  – предельная точка области определения   D   функции   f,   то  выражение   имеет смысл, причём  P_o  может быть как внутренней, так и граничной. Если же P_o – изолированная, то формально равенство  выполнено всегда, в изолированной точке все функции считаются непрерывными.

Точкой разрыва  будем называть любую предельную точку области определения функции, в которой нарушается непрерывность .

Из теоремы 6 и определения непрерывности сразу следует