Функции нескольких переменных. Множества в n-мерном евклидовом пространстве

9   ФУНКЦИИ  НЕСКОЛЬКИХ  ПЕРЕМЕННЫХ

Мы начинаем изучать математический анализ функций нескольких действительных переменных. Переход от случая одной переменной к случаю двух и большего числа переменных не совершается автоматически. Основные понятия – предел, производная, интеграл – приобретают здесь новые свойства и качества. Тем не менее, аналогия с более простым (и уже изученным) случаем нам очень поможет. Важно и то, что многие понятия и факты, рассматриваемые здесь для функций  n  переменных, при  n = 1  нам известны.

Функцией  n  переменных называется отображение

f :   D ® R , где R – поле действительных чисел, D – подмножество в  Rⁿ = { (x₁,..., x_n ) | x_iÎR }. Таким образом, функция  f = f(x₁,...,x_n) считается заданной, если задан закон, позволяющий для каждого упорядоченного набора чисел (x₁,...,x_n)ÎD находить единственное значение  f(x₁,...,x_n)ÎR.

9.1   Множества в  n–мерном евклидовом пространстве

9.1.1 Пространство Rⁿ. Областью определения всякой функции n переменных является некоторое множество упорядоченных наборов чисел, т. е. подмножество в Rⁿ.Поэтому начинать изучение таких функций нужно со знакомства с некоторыми видами подмножеств в  Rⁿ,с изучения их свойств.

Напомним, прежде всего, известные читателю сведения о самом пространстве Rⁿ. Множество  Rⁿ состоит из всех упорядоченных наборов действительных чисел:

Rⁿ = R´R´...´R = { (x₁, x₂,..., x_n) | x_iÎR }, т. е. является декартовым произведением  n  экземпляров множества  R  (см. АГ, раздел 1.1).

После введения операций сложения и умножения на число:

(x₁, x₂,..., x_n) + (y₁, y₂,..., y_n) = (x₁+y₁, x₂+y₂,..., x_n+y_n),

l(x₁, x₂,..., x_n) = (lx₁,lx₂,...,lx_n)

множество  Rⁿ  становится  линейным пространством  (АГ, 3.1, 3.3).

Далее, в пространстве   Rⁿ   вводится скалярное произведение.  Если x = (x₁,..., x_n), y = (y₁, y₂,..., y_n) –элементы  Rⁿ,то их скалярным произведением называется число

(x, y) = x₁y₁+x₂y₂+...+x_ny_n.

Конечномерное линейное пространство со скалярным произведением называется евклидовым пространством (АГ, 4.5, 7.5.1). Скалярное произведение позволяет ввести понятие  модуля  элемента  Rⁿ :

, а также понятие  расстояния  между элементами  Rⁿ :

.

В разделе  АГ, 4.5  было доказано неравенство Коши–Буняковского:

, справедливое для любых  x, y Î Rⁿ . Это неравенство позволяет определить  угол  между элементами  x, y :

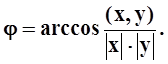
Установим справедливость ещё одного важного неравенства – «неравенства треугольника»:

Для доказательства проведём равносильные преобразования, используя определение модуля и свойства скалярного произведения:

Справедливость последнего соотношения следует из неравенства Коши – Буняковского.

Замечание. При  n = 2, n = 3  имеются хорошие геометрические интерпретации: элементы пространства  R²  удобно изображать точками плоскости, а элементы  R³ – точками трёхмерного пространства (после введения на плоскости и в пространстве прямоугольных декартовых систем координат). Изучая подмножества в Rⁿ , мы всегда будем обращаться к этим наглядным случаям. Очень часто можно разобраться в ситуации при  n = 2,  рассматривая множества на плоскости и определённые на них функции двух переменных, а затем перейти к общему случаю с помощью аналогии.

9.1.2   Открытые и замкнутые множества.  Пусть  aÎRⁿ.  Окрестностью  (или e–окрестностью) точки  a  называется множество

U_e(a) = { xÎRⁿ | | x–a | < e }.

Ясно, что при  n = 1  это  известная нам окрестность точки на числовой прямой –  интервал (a–e, a+e).  При  n = 2  это круг с центром  a  и радиусом  e,  не включающий границу, при n = 3  – шар с центром  a  радиусом  e,  не включающий ограничивающую его сферу.

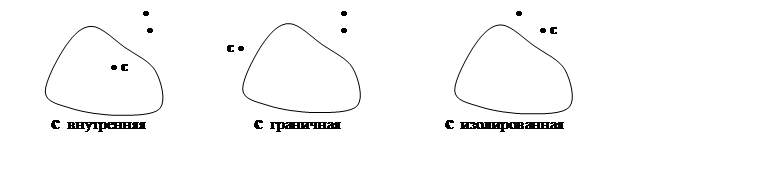
Пусть  MÍRⁿ. Точка  с  называется внутренней точкой множества  M, если существует окрестность  U_e(с), целиком лежащая в  M.  Если любая  U_e(с)  содержит и точки множества  M,  и точки, не лежащие в  M, то  с  называется граничной точкой M. Множество всех граничных точек называется  границей множества  M.  Если существует U_e(с), которая содержит только одну точку  M  – саму точку  c,  то такая точка называется изолированной.

Множество, все точки которого являются внутренними, называется открытым. Множество, дополнение к которому (т. е.  Rⁿ \ M) открыто, называется замкнутым. Замкнутые множества можно определять также с помощью понятия граничной точки.

Лемма 1.Множество  M  замкнуто   Û  M  содержит все свои граничные точки.

Доказательство.

«Þ». Пусть M замкнуто, с – граничная точка  M. Если  cÏM, то  c  лежит в дополнении к M. Но дополнение открыто, поэтому существует  U_e(с),целиком лежащая в дополнении. Это противоречит определению граничной точке. Значит, сÎM.

«Ü».  Пусть  M  содержит все свои граничные точки. Возьмём  cÏM.  Тогда  с  не является граничной, т. е. существует  U_e(с),  не пересекающаяся с  M.  Значит, любая точка дополнения является в нем внутренней, т. е. дополнение открыто. Следовательно M замкнуто.