Функции нескольких переменных. Множества в n-мерном евклидовом пространстве, страница 2

Простые свойства открытых и замкнутых множеств рассмотрены в теореме 1.

Теорема 1.    1) Объединение   любого числа открытых множеств является открытым множеством.

2) Пересечение 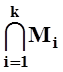  конечного числа открытых множеств является открытым множеством.

3) Пересечение любого числа замкнутых множеств замкнуто.

4) Объединение конечного числа замкнутых множеств замкнуто.

Доказательство.1) Возьмём xÎ. Тогда  $i:  xÎM_i.  Но  M_i   по условию открыто, т. е.  $U_e(x):  U_e(x) Í M_i.  Значит,  U_e(x) Í .  Итак, каждая точка входит в    вместе со своей окрестностью, т. е. является внутренней, что и требовалось доказать.

2) Возьмём . Так как  "i  xÎM_i,  а  M_i   открыто, то $e_i: .  Возмём    Тогда    для всех  i. Значит, 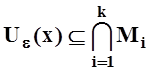, что и требовалось.

Пункты  3), 4)  доказываются так же просто.

Замечание. Утверждения пунктов 2) и 4) для бесконечного числа множеств несправедливы.  Например,  окрестность    –  открытое  множество  при  любом      n =1, 2, 3,....Однако 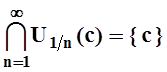 , а множество, состоящее из одной точки, очевидно, не является открытым.

9.1.3  Предел последовательности точек Rⁿ.Рассмотрим последовательность точек:

x₁,  x₂,  x₃,...,  x_k,...;       x_k ÎRⁿ .

Точка  aÎRⁿ  называется  пределом  последовательности  {x_k},  если

"e>0   $k₀:"k ³ k₀     | x_k – a |<e.

Используется обозначение:  ,  или проще:  a = lim x_k.  Связь с пределом числовой последовательности не только внешняя, как показывает

Теорема 2 (о покоординатной сходимости). Пусть {x_k} – последовательность точек  Rⁿ,  причём

x₁ = (x₁₁, x₁₂,..., x_1n),   x₂ = (x₂₁, x₂₂,..., x_2n),... ,  x_k = (x_k1, x_k2,..., x_kn),  ....

Пусть, кроме этого,  a = (a₁, a₂,..., a_n). Тогда

.

Другими словами,  a = lim x_k   равносильно тому, что первые координаты точек  x_k сходятся к первой координате  а,  вторые – ко второй,  и.т.д.

Доказательство.

« Þ ».  Дано:  a = lim x_k,т.е. "e>0  $k₀:"k ³ k₀  | x_k – a | < e.Но ясно, что

Значит,   "e>0  $k₀:"k³k₀ , т.е.  , что и требуется.

« Ü ». Дано: .   Можно записать это так:

 .

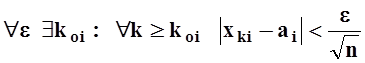Возьмём   k₀ = max { k_oi } . Тогда при  k ³ k₀:

.

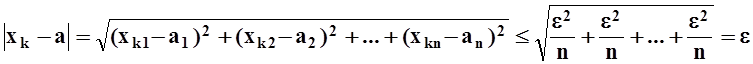Итак,    Теорема доказана.

Множество   MÍRⁿ  называется ограниченным, если , т. е.  если оно лежит в некоторой окрестности нулевой точки . Последовательность {x_n} называется ограниченной, если множество её значений ограничено. Как  и в случае числовых последовательностей, легко заметить, что всякая сходящая последовательность ограничена – почти все её члены лежат в окрестности точки, которая является пределом. Обратное неверно, однако справедлива

Теорема 3 (теорема Больцано – Вейерштрасса). Любая ограниченная последовательность точек  Rⁿ  содержит сходящуюся подпоследовательность.

Доказательство проведём для случая n = 2.   Пусть  (a₁, b₁), (a₂, b₂),...–ограниченная  последовательность  в    R².Рассмотрим   числовую   последовательность   a₁, a₂,..., a_k,.... Ограниченность  { (a_k, b_k) }  означает, что  Значит,   т.е. последовательность {a_k} ограничена. По теореме Больцано – Вейерштрасса для числовых последовательностей (теорема 8 из 1.4) в {a_k} существует сходящаяся подпоследовательность:  Рассмотрим соответствующие точки:

Их вторые координаты  образуют ограниченную числовую последовательность. Опять применяя теорему Больцано – Вейерштрасса для числовых последовательностей, выберем в ней сходящуюся подпоследовательность    и рассмотрим соответствующие точки

Так как числовые последовательности  сходятся, то, по теореме 2, сходится и выбранная подпоследовательность точек. Теорема доказана.