По условию он не равен 0 в точке P0, а значит (это следует из непрерывности рассматриваемых функций) и в некоторой её окрестности. Но тогда, как известно из линейной алгебры, переменные y1,...,yn можно выразить через x1,...,xn (например, по формулам Крамера). Следовательно, в этой окрестности существуют функции yi = ji(x1, ... , xn), неявно заданные системой (*).
Рассмотрим теперь вопрос о вычислении частных производных функций yi = ji(x1, ..., xn),заданных неявно системой (*). Пользуясь правилом дифференцирования сложных функций (теорема 13, 9.4.2), дифференцируем по x1 каждое из равенств (*):
,
…………………………………………………………..,
.
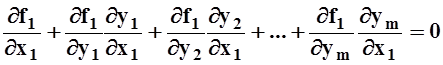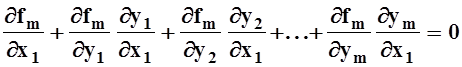Получилась система линейных
уравнений относительно 
. Её можно
решить, если определитель этой системы 
,
т.е. якобиан системы функций f1,
..., fm по
переменным y1,...,ym,не
равен в данной точке 0.
Пример 7. Функции y(x), z(x) заданы неявно системой равенств
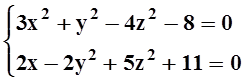
в окрестности точки (1, –3,
1). Найти
.
Решение.
Дифференцируем каждое равенство по x,
по правилу дифференцирования сложных функций: 
.
При x= 1 получается система линейных
уравнений: 
. Решая
её, находим: 
.
10.4 Условные экстремумы
Постановку задачи сначала поясним на примере .
Пример 8. На прямой 2x+y= 5 найти точку, в которой функция z= x2+y2 имеет локальный минимум.
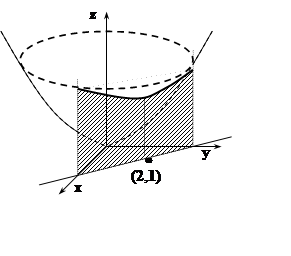Решение.
Обратим внимание: минимум функции z=x2+y2 требуется найти, рассматривая не
произвольные точки (x, y), а лишь те,
которые удовлетворяют условию (или уравнению
связи) 2x+y= 5. В данном
случае задача решается просто: используя уравнение связи, исключим одну из
переменных: y= 5–2x.
Получим функцию одной переменной:
z= x2+(5–2x)2 = 5x2–20x+25.
Её экстремумы находим по обычным правилам:
z¢=10x–20; 10x–20=0 Þx=2.
Так как z²=10, z²(2)> 0 , то x= 2 – точка минимума. Из уравнения связи находим: y = 5–2x= 1. Итак, (2, 1) – точка условного минимума.
Однако в более сложных задачах не всегда можно аналитически выразить одну переменную через другие. Кроме того, уравнений связи может быть несколько. Поэтому мы рассмотрим общий метод решения таких задач – метод множителей Лагранжа.Начнём с определения.
Пусть дана функция f(x1, ..., xn, y1, ..., ym) и уравнения связи:
(*)
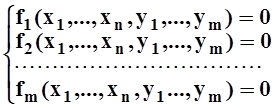Точка P0(x01,...,x0n,y01,...,y0m),удовлетворяющая условиям (*), называется точкой условного минимума функции f, если существует окрестность U точки P0 такая, что
"PÎU fi(P) = 0 (i = 1, ..., m) Þ f(P0) £ f(P).
Аналогично определяется и понятие условного максимума.
Для решения задачи о нахождении условных экстремумов рассмотрим так называемую функцию Лагранжа:
F(x1, …, xn, y1, … , ym, l1, … , lm) = f(x1, … , xn, y1, … , ym) +
fi(x1, … , xn, y1, … , ym).
Здесь новые переменные l1, … , lm называются множителями Лагранжа. Их количество равно числу уравнений связи. С помощью функции Лагранжа дадим необходимое условие условного экстремума.
Теорема
9. Пусть P0 – точка условного экстремума функции f(x1, … , xn, y1, … , ym) при условии (*), причём
якобиан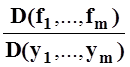 
(P0) ¹ 0. Тогда
существуют такие числа l1, l2, … , lm
, что частные производные первого порядка функции Лагранжа в точке P0 обращаются в 0.
Доказательство, чтобы упростить запись, проведём для m = n =2.
Итак, P0(x01, x02, y01, y02) – точка локального экстремума функции f(x1, x2, y1, y2), при условии
f1(x1, x2, y1, y2) = 0, f2(x1, x2, y1, y2) = 0.
Таккаквыполненыусловия теоремы8,тосуществуютфункции y1 =j1(x1,x2), y2=j2(x1,x2), заданные неявно условиями f1 = 0, f2 = 0. Рассмотрим функцию
(x1, x2) = f(x1, x2, j1(x1,x2),j2(x1,x2)).
Ясно, что (x01, x02) – точка экстремума
функции . Значит, частные производные 
, 
в
этой точке равны 0.
Вычислим сначала производную по x1,
используя правило дифференцирования сложных функций:
(x01, x02) =
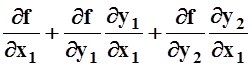= 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.