Функции нескольких переменных. Формула Тейлора, страница 2

Точки, в которых  df(P₀)º0, называются стационарными. Из теоремы 2 следует, что функция может иметь экстремум только в стационарной точке. Однако не обязательно стационарная точка является точкой экстремума – условие теоремы 2 необходимо, но не достаточно.

Пример 1. Рассмотрим функцию  f(x, y)= x² – y².  Её частные производные    обращаются в  0  в точке(0, 0) . Значит, (0, 0) – стационарная точка. Однако ни максимума, ни минимума в этой точке нет. Действительно, f(0, 0)= 0.  Но в любой окрестности точки (0, 0) функция   f(x, y) = x² – y² принимает и положительные (при x¹ 0, y= 0), и отрицательные  (при x= 0,  y¹0)  значения.  (Графиком   этой функции является гиперболический параболоид – седловидная поверхность,  имеющая уравнение  z = x² – y²).

Чтобы сформулировать достаточные условия экстремума, нужно использовать второй дифференциал. Как мы знаем, второй дифференциал функции f(x₁,x₂,...,x_n) в точке P₀  является квадратичной формой от приращений переменных:

.

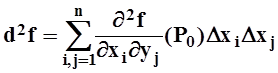Здесь значения вторых производных (т.е. числа),  приращения переменных. Напомним определение из курса алгебры: квадратичная форма называется положительно определённой (отрицательно определённой), если она принимает только положительные (отрицательные) значения (кроме случая, когда все переменные равны 0– тогда и значение формы, конечно, равно 0). Квадратичная форма называется неопределённой, если она принимает и положительные, и отрицательные значения (подробнее см. АГ, раздел 7.4).

Теорема 3 (достаточные условия локального экстремума). Пусть в некоторой окрестности U стационарной точки P₀ функция f(x₁,...,x_n) имеет непрерывные частные производные до 3–го порядка включительно. Второй дифференциал d²f(P₀) рассматриваем как квадратичную форму от приращений . Если эта форма положительно определена, то P₀ – точка минимума, если отрицательно определена, то P₀ – точка максимума.  Если  d²f  является неопределённой квадратичной формой, то экстремума в точке  P₀  нет.

Доказательство. Запишем формулу Тейлора для функции f в окрестности точки P₀ до второго дифференциала включительно:

.

По условию,  P₀ – стационарная точка, т.е.  df(P₀)º0,поэтому

.

Нас интересует знак выражения в квадратных скобках. Если это выражение положительно (в некоторой окрестности P₀ ), т.е. f(P) ³ f(P₀), то ясно, что P₀ – точка локального минимума. Аналогично, если это выражение отрицательно, то f(P) £ f(P₀) и  P₀ – точка максимума. Если же  может принимать разные знаки в любой, даже очень малой окрестности  P₀ ,  то очевидно, что экстремума в точке  P₀  нет.

Рассуждая нестрого, можно сказать что 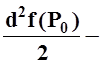  бесконечно малая 2 порядка относительно приращений  (так как это квадратичная форма). А (как доказано выше), т.е. имеет более высокий порядок малости. Поэтому знак суммы     определяется знаком первого слагаемого. Отсюда сразу следует справедливость теоремы.

Проведём строгое доказательство  последнего замечания для случая функции двух переменных f(x₁,x₂). Однако выберем способ рассуждений, справедливый и в общем случае.

Обозначим  .  Пусть   –положительно определённая квадратичная форма. Преобразуем:

.

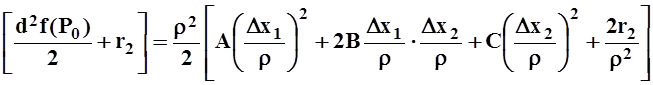Функция 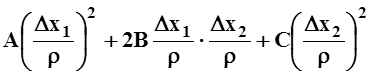определена на окружности радиуса 1 с центром в точке (0, 0).  Действительно, при любых  

.

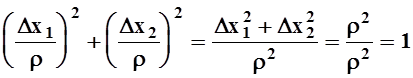Окружность является ограниченным и замкнутым (т.е. компактным) множеством. Поэтому непрерывная функция на ней достигает своей точной нижней грани a. Из положительной определённости  d²f(P₀) следует, что это число – положительно:

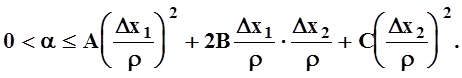
Так как 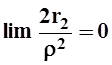 при , то ясно, что при малых  выражение  будет меньше  a,  а значит будет положительным выражение

.

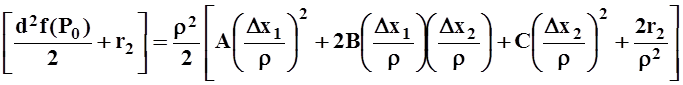Следовательно,  P₀ – точка минимума.

Случай отрицательно определённой формы   d²f(P₀)в точности аналогичен.

Пусть теперь  d²f(P₀) – неопределённая форма. Возьмём такие числа  t₁, t₂,  что d²f(P₀)>0при  .  Посмотрим, каким будет знак выражения ,  если изменять значения переменных:   ,  причём  e®0.    Так как