Исследование переходных процессов в линейных цепях. Моделирование переходных процессов на ПК. Обработка графиков, страница 12

Рис.7.20. Графики переходного процесса в цепи R-C

Используя графики, найдите величину постоянной времени – τ.

    Примечание: Вопросы для зачета по 1^ой схеме в конце 7-ой лабораторной работы.

Приступим к выполнению пункта №3

3. ИССЛЕДОВАНИЕ ЦЕПИ R-L ПРИ ВКЛЮЧЕНИИ НА СИНУСОИДАЛЬНОЕ НАПРЯЖЕНИЕ

A.Теоретические сведения.

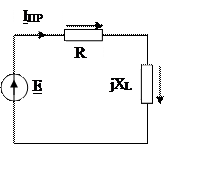
Исходная схема имеет вид (рис.7.21). Обсудим расчет этой схемы. В рассматри

R

                                             аемой (послекоммутационной) схеме, одна ветвь, один                                             

Кл

                                            контур. Следовательно, можно составить одно уравнен

L

е(t)

                                            ие по 2-ому закону Кирхгофа для мгновенных значении:

i(t)

                                                                                                    (7.11)

                                            Если сравнить уравнение (7.1) и (7.11),  то они отличают.Рис.7.21 Цепь R-L.      ся только правой частью. Напомним, что от вида правой части зависит только одна (из двух) составляющая решения линейного дифференциа-льного уравнения- принужденная часть решения. Если для решения уравнения (7.11) использовать классический метод, то очевидно, весь порядок остается без изменения.

Необходимо лишь заново рассчитать принужденный режим. Поэтому, пропуская 1-ый пункт (Нахождение корней характеристического уравнения), приступим сразу ко 2-ому пункту: Расчет принужденного режима (t→ ∞).

URПР

Характер принужденного режима в линейной цепи определяется видом э.д.с. В рассматриваемом случае e(t)=E_msin(ωt+φ), т.е. это синусоидальная функция. Но, если э.д.с. меняется по синусоидальному закону, то расчет принужденного режима следует выполнить символическим методом (см. лаб.раб. №2). Расчетная схема принужденного режима показана на ( рис.7.22). По закону Ома в символической фор                                               ме получим

ULПР

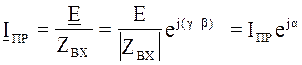                                                                  ,              (7.12)

где Z_ВХ=R+jX_L=,

,

Рис.7.22 Схема к п.2                                U_LПР =I_ПРjX_L=I_ПРjωL=I_ПРωLe^j(α+90)             (7.13)

Комплексу тока (7.12) соответствует функция времени: i_ПР(t)=I_ПРsin(ωt+α)   (7.14)

Комплексу напряжения (7.13) : u_LПР(t)= I_ПРωLsin(ωt+α+90^○)                            (7.15)

3-ий пункт: Записываем решения для искомых токов и напряжении.

Решение уравнения (7.1) в классическом методе ищут в виде суммы двух слагаемых:

i(t)=i_ПР(t)+ i_СВ(t)  и   u_L(t)= u_LПР(t)+ u_{L СВ}(t)

С учетом результатов п.2 (7.14, 7.15),  эти выражения примут вид:

i(t)= = I_ПРsin(ωt+α) + i_СВ(t)     u_L(t)= I_ПРωLsin(ωt+α+90^○)+ u_{L СВ}(t)

Вид свободных составляющих зависит от числа и характера корней характеристичес-кого уравнения (7.2). Так как корень один, то решения  следует искать в виде:

i(t)= I_ПРsin(ωt+α) +A₁e^pt  u_L(t)= I_ПРωLsin(ωt+α+90^○)+ A₂e^pt, где        (7.16)                      

A₁, A₂- постоянные интегрирования, подлежащие определению. Для этого, прежде всего запишем (7.16) в момент коммутации, т.е при t=0. Получим:

i(0)= I_ПРsin(α)  +A₁ ,      u_L(0)= I_ПРωLsin(α+90^○)+ A₂ , где              (7.17)

i(0), u_L(0)- начальные значения (условия) тока в цепи и напряжения на индуктивности в момент коммутации. Найдя i(0), u_L(0), определим A₁, A₂.

4-ый пункт: Рассчитываем независимые начальные условия.