2.118. Дакажыце, што для функцыі Дырыхле
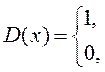
![]()
![]()
![]()
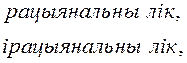 не існуе ліміт ні ў адным пункце.
не існуе ліміт ні ў адным пункце.
2.119. Вылічыце наступныя ліміты:
1) ![]() ; 2)
; 2) 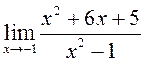 ; 3)
; 3) 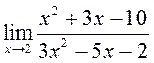 ; 4)
; 4) 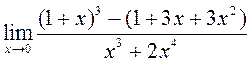 ; 5)
; 5) 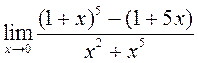 ; 6)
; 6) 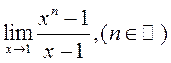 ; 7)
; 7) 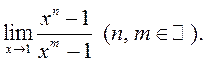
2.120. Знайдзіце ліміты:
1) 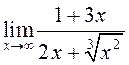 ; 2)
; 2) 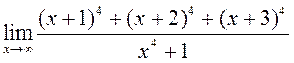 ;
3)
;
3) 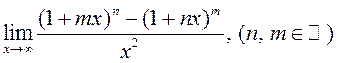 ; 4)
; 4) 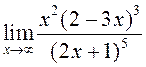 ; 5)
; 5) 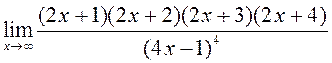 ; 6)
; 6) 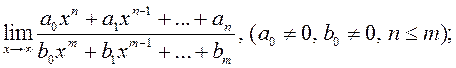 7)
7) 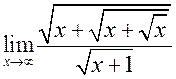 ; 8)
; 8) 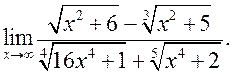
2.121. Знайдзіце ліміты:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]()
2.122. Сфармулюйце з дапамогай няроўнасцяў наступныя сцверджанні і дайце
адпаведныя прыклады:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
2.123. Няхай ![]() а
а ![]() Дакажыце, што:
1)
Дакажыце, што:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) 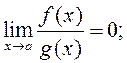 4) Што можна сцвярджаць пра ліміт здабытку
4) Што можна сцвярджаць пра ліміт здабытку ![]()
2.124. Дакажыце, што наступныя ліміты не існуюць:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]()
2.125.
Прывядзіце прыклад функцыі ![]() , для якой
існуе
, для якой
існуе ![]() і не існуе
і не існуе ![]() .
.
2.126. Ці існуе ![]() ,
калі:
1)
,
калі:
1) ![]()
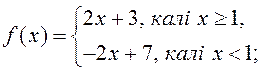 2)
2) ![]()
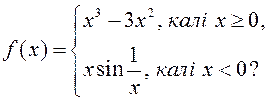
2.127. Няхай 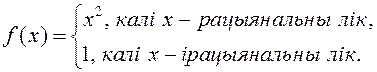 Знайдзіце пункты, ў якіх гэтая функцыя мае ліміт.
Знайдзіце пункты, ў якіх гэтая функцыя мае ліміт.
2.128. Знайдзіце ліміты:
1) 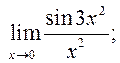 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() 5)
5) 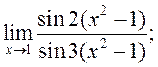 6)
6) ![]() 7)
7) ![]() 8)
8) 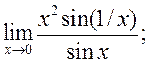 9)
9) 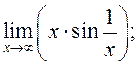 10)
10) ![]() 11)
11) ![]() 12)
12) ![]() 13)
13) ![]()
2.129. Знайдзіце: 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() 5)
5) 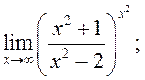 6)
6) ![]()
2.130. Дакажыце, што не заўсёды выконваецца
наступнае сцверджанне пра ліміт складанай функцыі: калі ![]() а
а ![]() , тады і
, тады і ![]() Разгледзьце
прыклад:
Разгледзьце
прыклад:
![]()
![]()
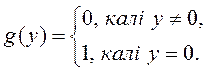 Параўнайце прыведзенае сцверджанне з тэарэмай пра ліміт скла-данай функцыі.
Параўнайце прыведзенае сцверджанне з тэарэмай пра ліміт скла-данай функцыі.
Няхай ![]() вызначана
ў некаторым ваколлі пункта
вызначана
ў некаторым ваколлі пункта ![]() .
Функцыя
.
Функцыя ![]() называецца непарыўнай
у пункце а, калі
называецца непарыўнай
у пункце а, калі ![]()
![]() . Карыстаючыся
азначэннем ліміта функцыі паводле Кашы, атрымаем: функцыя
. Карыстаючыся
азначэннем ліміта функцыі паводле Кашы, атрымаем: функцыя ![]() ёсць
непарыўная ў пункце
ёсць
непарыўная ў пункце ![]() ,
калі
,
калі
![]() .
.
Функцыю называюць непарыўнай на мностве ![]() калі яна
непарыўная ў кожным пункце гэтага мноства.
калі яна
непарыўная ў кожным пункце гэтага мноства.
Калі існуюць ![]() ,
, ![]() , прычым
, прычым ![]() =
=![]() =
=![]() ,
то
,
то ![]() ёсць
непарыўная ў пункце
ёсць
непарыўная ў пункце ![]() .
Гэтую акалічнасць часта скарыстоўваюць пры даследаванні непарыўнасці функцый,
зададзеных рознымі формуламі на розных мноствах.
.
Гэтую акалічнасць часта скарыстоўваюць пры даследаванні непарыўнасці функцый,
зададзеных рознымі формуламі на розных мноствах.
Непарыўнасць складанай функцыі: з непарыўнасці функцыі ![]() у пункце
у пункце ![]() і непарыўнасці
функцыі
і непарыўнасці
функцыі ![]() у пункце
у пункце ![]() вынікае
непарыўнасць складанай функцыі
вынікае
непарыўнасць складанай функцыі ![]() у
пункце
у
пункце ![]() .
.
Асноўныя элементарныя функцыі: ![]() ,
, ![]() ,
, ![]() , трыганаметрыч-ныя
і адваротныя трыганаметрычныя функцыі з’яўляюцца непарыўнымі ў пунктах іх
вызначэння.
, трыганаметрыч-ныя
і адваротныя трыганаметрычныя функцыі з’яўляюцца непарыўнымі ў пунктах іх
вызначэння.
Няхай ![]() вызначана
ў некаторым ваколлі пункта
вызначана
ў некаторым ваколлі пункта ![]() ,
за выключэн-нем, магчыма, самога пункта
,
за выключэн-нем, магчыма, самога пункта ![]() . Пункт
. Пункт ![]() называюць:
1) пунктам скасавальнага разрыву, калі існуе
называюць:
1) пунктам скасавальнага разрыву, калі існуе ![]() , але
, але ![]() або
або ![]() не вызначана ў
пункце
не вызначана ў
пункце ![]() ;
2) пунктам разрыву тыпу скачка, калі існуюць аднабаковыя
ліміты, але
;
2) пунктам разрыву тыпу скачка, калі існуюць аднабаковыя
ліміты, але ![]() .
Пункты разрыву абодвух гэтых тыпаў называюць таксама пунктамі разрыву першага
тыпу;
3) пунктам разрыву другога тыпу, калі прынамсі адзін з
аднабако-вых лімітаў не існуе або бясконцы.
.
Пункты разрыву абодвух гэтых тыпаў называюць таксама пунктамі разрыву першага
тыпу;
3) пунктам разрыву другога тыпу, калі прынамсі адзін з
аднабако-вых лімітаў не існуе або бясконцы.
Функцыю ![]() называюць
раўнамерна непарыўнай на мностве
называюць
раўнамерна непарыўнай на мностве ![]() , калі
, калі ![]() >0
>0 ![]() :
: ![]() ,
, ![]()
![]()
![]() . Падкрэслім,
што адрозненне раўнамернай непарыўнасці функцыі на мностве
. Падкрэслім,
што адрозненне раўнамернай непарыўнасці функцыі на мностве ![]() ад
непарыўнасці на гэтым мностве ў тым, што ў азначэнні раўнамернай непарыўнасці
ад
непарыўнасці на гэтым мностве ў тым, што ў азначэнні раўнамернай непарыўнасці ![]() залежыць
толькі ад
залежыць
толькі ад ![]() і не залежыць
ад
і не залежыць
ад ![]() .
.
Тэарэма Кантара. Непарыўная на адрэзку функцыя ёсць раўнамерна непарыўная на гэтым адрэзку.
Прыклад 1. Даследаваць на непарыўнасць і вызначыць тып
пунктаў разрыву функцыі 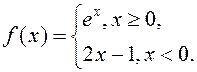
►Возьмем адвольны пункт ![]() і
дакажам непарыўнасць
і
дакажам непарыўнасць ![]() у
гэтым пункце. Разгледзім
у
гэтым пункце. Разгледзім ![]() – акругу пункта
– акругу пункта ![]() , дзе
, дзе ![]() задавальняе
ўмову
задавальняе
ўмову ![]() . У гэтай
акрузе
. У гэтай
акрузе ![]() супадае з
функцыяй
супадае з
функцыяй ![]() , калі
, калі ![]() , або з
функцыяй
, або з
функцыяй ![]() , калі
, калі ![]() . Абедзве гэтыя
функцыі (як элементарныя) непарыўныя ў пункце
. Абедзве гэтыя
функцыі (як элементарныя) непарыўныя ў пункце ![]() . Засталося
даследаваць непарыўнасць
. Засталося
даследаваць непарыўнасць ![]() у
пункце
у
пункце ![]() . Паколькі
. Паколькі ![]() злева і справа
ад гэтага пункта вызначаецца рознымі формуламі, то разгледзім аднабаковыя
ліміты гэтай функцыі ў пункце
злева і справа
ад гэтага пункта вызначаецца рознымі формуламі, то разгледзім аднабаковыя
ліміты гэтай функцыі ў пункце ![]() .
Маем:
.
Маем: ![]() , а
, а ![]() . Паколькі
аднабаковыя ліміты існуюць, але няроўныя паміж сабой, заключаем, што ў пункце
. Паколькі
аднабаковыя ліміты існуюць, але няроўныя паміж сабой, заключаем, што ў пункце ![]() функцыя мае
разрыў першага тыпу. ◄
функцыя мае
разрыў першага тыпу. ◄
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.