Ліміты і непарыўнасць. Лікавыя функцыі і паслядоўнасці. Незалежнай зменнай або аргументам функцыі, страница 6

2.111. З дапамогай крытэра Кашы дакажыце наступнае сцверджанне: для таго каб камплексная паслядоўнасць () была збежнай, неабходна і дастаткова, каб яна была фундаментальнай.

2.3. ЛІМІТ ФУНКЦЫІ.

Няхай  вызначана ў працятым ваколлі пункта . Лік  называ-ецца лімітам функцыі  у пункце  (), калі  : ,  (азначэнне паводле Кашы).

Прыведзенае азначэнне раўназначнае наступнаму:  калі для адвольнай паслядоўнасці (), , збежнай да , мае месца роўнасць  (азначэнне паводле Гайнэ).

Калі ў азначэнні Кашы няроўнасць  замяніць няроўнасцямі  або  то лік  называюць адпаведна правабаковым або левабаковым лімітам функцыі  у пункце . Для аднабаковых лімітаў выкарыстоўваюць адпаведна абазначэнні:  і  або  і .

Запіс  азначае:  : ,  .

    Грунтоўныя ліміты:                 

    Тэарэма 1. Калі ,  то: а) ;     б) ; в)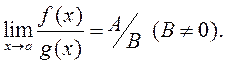 

    Тэарэма 2. Калі ў некаторым ваколлі пункта   і  тады і

    Тэарэма 3 (пра ліміт складанай функцыі). Няхай існуюць  ( калі  і , тады існуе ліміт складанай функцыі  пры , прычым

Апошняя тэарэма дазваляе пры вылічэнні лімітаў пераходзіць ад зменнай  да новай зменнай  дзе .

    Прыклад 1. Даказаць, што

►Для таго каб даказаць, што , зыходзячы з азначэння Кашы, звычайна дзейнічаюць наступным чынам: разглядаюць велічыню  і ацэньваюць яе зверху, імкнучыся атрымаць ацэнку выгляду

               (канстанта).                      (2.1)

Пры гэтым, паколькі ў азначэнні ліміту дастаткова ўказаць не абавязкова максімальнае значэнне , то звычайна абмяжоўваюць  зверху, да прыкладу, лічаць , г. зн. няроўнасць (2.1) разглядаюць толькі для  Калі цяпер узяць  то для ўсіх  атрымаем:

У разгляданым прыкладзе будзем лічыць  г.зн. будзем браць  З такіх меркаванняў маем:   Тады  дастаткова ўзяць , каб ,  атрымаць  што і патрабавалася.

Можна скарыстаць і другое азначэнне ліміту функцыі. Возьмем ,  Патрэбна даказаць, што  

Сапраўды,   ◄

    Прыклад 2. Даказаць, што  не існуе.

►Для доказу неіснавання ліміту зручна карыстацца азначэннем Гайнэ. У адпаведнасці з ім дастаткова пабудаваць паслядоўнасць (),збежную да , , для якой () разбягаецца, або знайсці дзве паслядоўнасці  і , збежныя да , такія, што адпаведныя паслядоўнасці значэнняў функцыі  і  маюць розныя ліміты. У дадзеным прыкладзе дастаткова знайсці , збежную да нуля,  і такую, што паслядоўнасць  разбягаецца. Паслядоўнасць  задавальняе патрэбныя ўмовы, а адпаведная паслядоўнасць значэнняў функцыі  відавочна разбягаецца. Адсюль вынікае, што  не існуе. ◄

    Прыклад 3. Знайсці

►Паколькі  то мы маем нявызнача-насць тыпу  . Пры  раскрыцці такіх нявызначасцяў, а таксама нявыз-начасцяў тыпу , , выкарыстоўваюць тыя ж метады, што і ў ана-лагічных абставінах для паслядоўнасцяў.  Істотна,  што пры  разглядзе ліміту функцыі пры  аргумент  не набывае значэння . Тады мы можам скараціць дроб на  і атрымаць             . ◄

    Прыклад 4. Знайсці

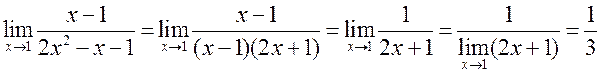►Калі ўзяць 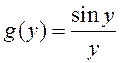, а  то атрымаем  Паколькі  прычым  для  то на падставе тэарэмы пра ліміт складанай функцыі маем: 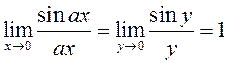 (скарысталі першы грунтоўны ліміт ).  ◄

ЗАДАЧЫ

2.112. Сфармулюйце азначэнні (паводле Кашы і Гайнэ) ў дадатным сэнсе наступнага сцверджання:

2.113.  Карыстаючыся азначэннем Гайнэ, дакажыце тэарэму пра ліміт сумы, розніцы, здабытку, дзелі дзвюх функцый.

2.114.  1) Дакажыце, што калі , то 2) Ці выконваецца адваротнае сцверджанне ?

2.115.  Дадзены функцыя  і лікі  і . Для адвольнага  знайдзі-це найбольшы  каб для ўсіх , што задавальняюць умову , праўдзілася няроўнасць : 1) ;  2) 

2.116.  Карыстаючыся азначэннем Кашы, дакажыце, што: 1) ;     2) 

2.117.  Знайдзіце наступныя ліміты, карыстаючыся азначэннем Гайнэ і ўласцівасцямі паслядоўнасцяў: 1) 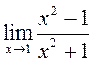;         2) ;        3) ;  4) ;  5)