Тэарэма. Няхай функцыя ![]() ёсць
строга манатонная і непарыўная на прамежку Т і функцыя
ёсць
строга манатонная і непарыўная на прамежку Т і функцыя ![]() – яе адваротная функцыя. Няхай
функцыя
– яе адваротная функцыя. Няхай
функцыя ![]() дыферэнцавальная ў пункце
дыферэнцавальная ў пункце ![]() , прычым.
, прычым. ![]() , а функцыя
, а функцыя ![]() – вызначаная на прамежку Т
і дыферэнцавальная ў пункце
– вызначаная на прамежку Т
і дыферэнцавальная ў пункце![]() . Тады
складаная функцыя
. Тады
складаная функцыя ![]() ,якая вызначаецца
роўнасцямі (1), ёсць дыферэнцавальная ў пункце
,якая вызначаецца
роўнасцямі (1), ёсць дыферэнцавальная ў пункце ![]() і
і
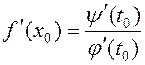 .
.
□ На падставе тэарэмы пра дыферэнцавальнасць
адваротнай функцыі, функцыя ![]() ёсць
дыферэнцавальная ў пункце
ёсць
дыферэнцавальная ў пункце ![]() і
і
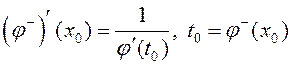 .
(2)
.
(2)
Згодна з тэарэмаю пра дыферэнцавальнасць складанай функцыі функцыя ![]() ёсць
дыферэнцавальная ў пункце
ёсць
дыферэнцавальная ў пункце ![]() , прычым
, прычым
 . ■
. ■
Такім чынам, маем формулу
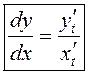 , дзе
, дзе ![]() .
.
![]() .
(3)
.
(3)
(Зазначым, што функцыя ![]() неманатонная
на
неманатонная
на ![]() , але манатонная як на
, але манатонная як на  , так і на
, так і на  . Што за крывая?)
. Што за крывая?)
► 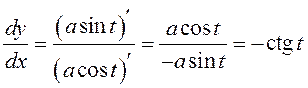 . З другога боку, калі з
роўнасцяў (3) выключыць параметр t, то
. З другога боку, калі з
роўнасцяў (3) выключыць параметр t, то ![]() , адкуль атрымаецца функцыя
, адкуль атрымаецца функцыя ![]() , вытворная якой
, вытворная якой 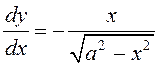 . Улічваючы роўнасці (3),
маем
. Улічваючы роўнасці (3),
маем 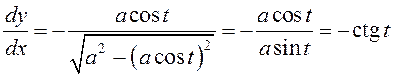 . ◄
. ◄
Вытворная другога парадка функцыі, зададзенай параметрычна, вылічаецца наступным чынам:
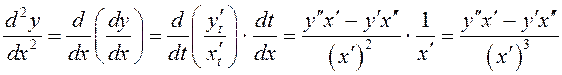 .
.
Аналагічна вылічаюцца вытворныя наступных парадкаў.
2º. Няяўная функцыя.
Няхай Е—мноства пунктаў ![]() плоскасці
плоскасці ![]() . Калі кожнаму пункту
. Калі кожнаму пункту ![]() ставіцца ў адпаведнасць
паводле некаторага правіла лік
ставіцца ў адпаведнасць
паводле некаторага правіла лік ![]() , то
кажуць, што на мностве Е зададзена лікавая функцыя ад дзвюх зменных
х і у:
, то
кажуць, што на мностве Е зададзена лікавая функцыя ад дзвюх зменных
х і у: ![]() .
.
Напрыклад, аб’ём конуса ![]() ёсць функцыя дзвюх зменных r і h.
ёсць функцыя дзвюх зменных r і h.
Няхай прамавугольнік ![]() змяшчаецца ў абсягу
вызначэння функцыі
змяшчаецца ў абсягу
вызначэння функцыі ![]() і няхай
і няхай ![]() . Калі на адрэзку
. Калі на адрэзку ![]() існуе функцыя
існуе функцыя ![]() такая, што
такая, што ![]() і
і ![]() , то кажуць, што раўнанне
, то кажуць, што раўнанне ![]() вызначае на прамавугольніку
вызначае на прамавугольніку
![]() у як няяўную функцыю
зменнай x.
у як няяўную функцыю
зменнай x.
Напрыклад, раўнанне ![]() вызначае
дзве няяўныя функцыі
вызначае
дзве няяўныя функцыі ![]() .
.
Пытанне аб умовах існавання няяўнай функцыі будзем высвятляць у другім семестры.
Калі прадыферэнцаваць тоеснасць ![]() як складаную функцыю, можна
атрымаць вытворную
як складаную функцыю, можна
атрымаць вытворную ![]() .
.
 .
.Тэарэма Бальцана-Кашы (аб прамежкавым значэнні). Калі функцыя f ёсць непарыўная на адрэзку ![]() і
і ![]() , то для кожнага рэчаіснага
ліку γ , які размяшчаецца паміж f(a) і f(b), існуе прынамсі адзін пункт
, то для кожнага рэчаіснага
ліку γ , які размяшчаецца паміж f(a) і f(b), існуе прынамсі адзін пункт ![]()
□ Няхай для пэўнасці ![]() . Разгледзім дапаможную
функцыю
. Разгледзім дапаможную
функцыю ![]() , якая непарыўная на
, якая непарыўная на ![]() і
і ![]() . Для доказу тэарэмы
дастаткова паказаць, што існуе пункт
. Для доказу тэарэмы
дастаткова паказаць, што існуе пункт ![]()
Няхай ![]() .
Гэтае мноства непустое
.
Гэтае мноства непустое ![]() і абмежаванае
зверху, напрыклад, лікам b. Згодна з тэарэмаю пра межы існуе лік
і абмежаванае
зверху, напрыклад, лікам b. Згодна з тэарэмаю пра межы існуе лік ![]() .
Паколькі
.
Паколькі ![]() , то на падставе тэарэмы пра
стабілізацыю знаку існуе поўінтэрвал
, то на падставе тэарэмы пра
стабілізацыю знаку існуе поўінтэрвал ![]() , на якім
, на якім
![]() і таму
і таму ![]() . Аналагічна атрымліваецца,
што
. Аналагічна атрымліваецца,
што ![]() . Гэта азначае, што
. Гэта азначае, што ![]()
Пакажам, што ў гэтым пункце ![]() .
Сапраўды, калі дапусціць процілеглае, што
.
Сапраўды, калі дапусціць процілеглае, што ![]() ,
то існуе акруга пункта
,
то існуе акруга пункта ![]() , дзе
, дзе ![]() захоўвае знак
захоўвае знак ![]() . Але справа ад
. Але справа ад ![]() функцыя
функцыя ![]() , а злева, згодна з
азначэннем
, а злева, згодна з
азначэннем ![]() , у кожнай акрузе існуе
пункт, у якім
, у кожнай акрузе існуе
пункт, у якім ![]() . Гэта значыць,
што
. Гэта значыць,
што
![]() .
.
Такім чынам, ![]() .
(Як правесці доказ у выпадку
.
(Як правесці доказ у выпадку ![]() ?
? ![]() ) ■
) ■
|
Няхай функцыя |
Функцыя |
Але ўмова непарыўна-сці не з’яўляецца неабходнаю
для існа-вання |
Першая тэарэма Ваерштраса (пра абмежаванасць функцыі). Калі функцыя f ёсць непарыўная на адрэзку ![]() , то яна абмежаваная на
гэтым адрэзку, г.зн.
, то яна абмежаваная на
гэтым адрэзку, г.зн. ![]() .
.
□ (ад процілеглага) Няхай f – неабмежаваная
на ![]() ,
г. зн.
,
г. зн.
![]() .
.
Возьмем ![]() і
пабудуем
і
пабудуем ![]() лікавую паслядоўнасць
лікавую паслядоўнасць ![]()
![]() , г. зн.
, г. зн. ![]() . Паколькі
. Паколькі ![]() – абмежаваная
– абмежаваная ![]() , то згодна з тэарэмаю
Бальцана-Ваерштраса (прынцып выбару) з яе можна вылучыць збежную
падпаслядоўнасць
, то згодна з тэарэмаю
Бальцана-Ваерштраса (прынцып выбару) з яе можна вылучыць збежную
падпаслядоўнасць ![]() . Няхай
. Няхай ![]() –яе ліміт. Паколькі
–яе ліміт. Паколькі ![]() , то з тэарэмы пра лімітавы
пераход у няроўнасці маем
, то з тэарэмы пра лімітавы
пераход у няроўнасці маем ![]() .
Паколькі f –непарыўная у пункце
.
Паколькі f –непарыўная у пункце ![]() ,
то
,
то ![]() , але гэта немагчыма,
паколькі
, але гэта немагчыма,
паколькі ![]() –бясконца вялікая
паслядоўнасць як падпаслядоўнасць бясконца вялікай паслядоўнасці
–бясконца вялікая
паслядоўнасць як падпаслядоўнасць бясконца вялікай паслядоўнасці ![]() . Такім чынам, дапушчэнне
непраўдзівае, а тым самым f – абмежаваная. ■
. Такім чынам, дапушчэнне
непраўдзівае, а тым самым f – абмежаваная. ■
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.