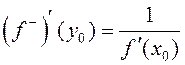Дыферэнцыяльнае злічэнне. Вытворная і дыферэнцыял. Адпаведна левабаковай і правабаковай вытворнымі функцыі, страница 2

Тэарэма 2. Калі строга манатонная і непарыўная на прамежку Х функцыя  ёсць дыферэнцавальная ў пункце  і , то адваротная функцыя  ёсць таксама дыферанцавальная ў адпаведным пункце   і яе вытворная ёсць .

□ На падставе тэарэмы пра адваротную функцыю, функцыя  ёсць непарыўная на прамежку . Таму пры  мае месца . Маем 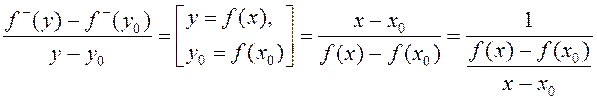. Пры пераходзе да ліміту пры  (пры гэтым ) маем .■

§3.3. Формулы дыферэнцавання.

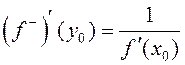1º. Паказнікавая і лагарыфмічная функцыі.

Пры вылічэнні вытворнай паказнікавай функцыі  будзем карыстацца лімітам 2º. §2.12. :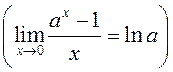 

.

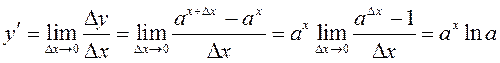Такім чынам, 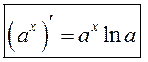 .   У прыватнасці .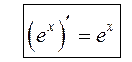

Паколькі функцыя  ёсць адваротная для функцыі , то

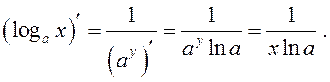
Такім чынам, 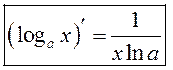  .  У прыватнасці  .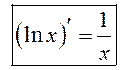

2º. Ступеневая функцыя.

Пры вылічэнні вытворнай ступенвай функцыі  будзем карыстацца лімітам 3º. §2.12: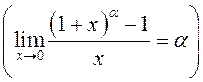  

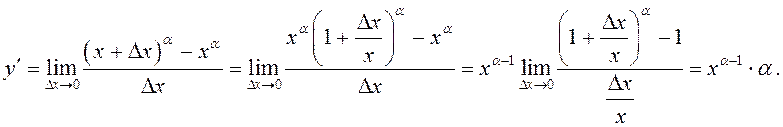
Такім чынам,

 .

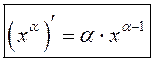3º. Трыганаметрычныя функцыі.

  

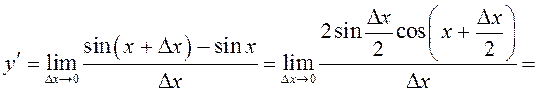
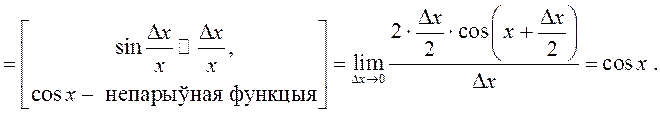
Такім чынам,   .  Аналагічна   .

Пры вылічэнні вытворнай функцыі  карыстаемся правілам вылічэння вытворнай дзелі:

 .

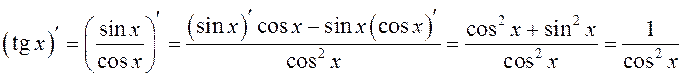Такім чынам, 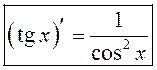 .   Аналагічна   .

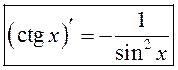4º. Адваротныя трыганаметрычныя функцыі. 

Паколькі  ёсць адваротная для функцыі , то паводле тэарэмы пра вытворную для адваротнай функцыі:

 .

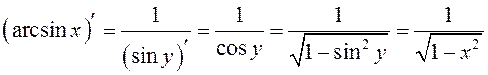Такім чынам, 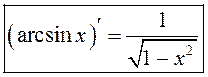 .  Аналагічна   .

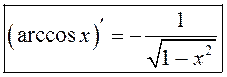Паколькі  ёсць адваротная для функцыі , то паводле тэарэмы пра вытворную для адваротнай функцыі:

 .

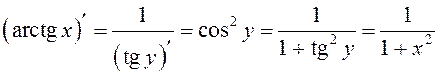Такім чынам, 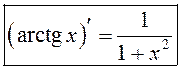 .  Аналагічна  .

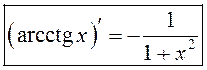5º. Гіпербалічныя функцыі.

Дастасоўваючы правілы вылічэння вытворнай да функцыі , маем:

.

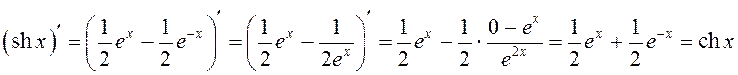Такім чынам,  .  Аналагічна  .

Карыстаючыся формулаю вылічэння вытворнай дзелі, маем:

 .

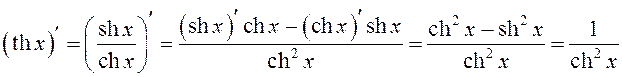Такім чынам, 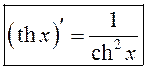 .  Аналагічна   .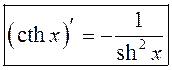

Як і ў выпадку адваротных трыганаметрычных функцый маем:

 .

 .

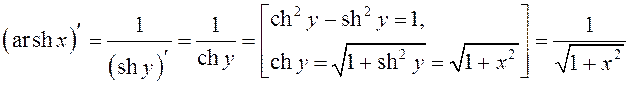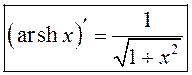, або .

 .

 .

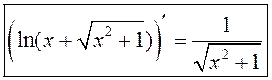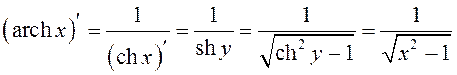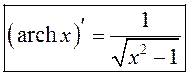  або .

 .

 .

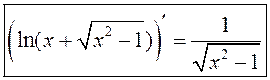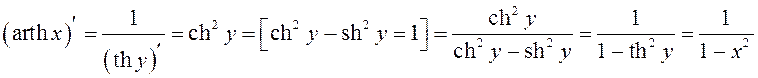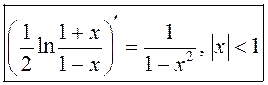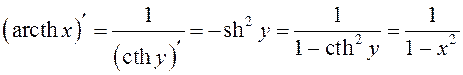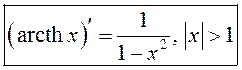, або .

.

 . 

 , або .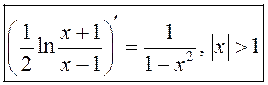

Такім чынам, маем .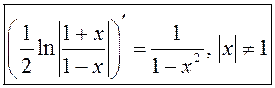

§3.4. Дыферэнцаванне складанай функцыі.

Тэарэма 1 (пра дыферэнцаванне складанай функцыі). Калі функцыя  ёсць дыферанцавальная ў пункце , а функцыя  – дыферэнцавальная ў пункце , дзе , то складаная функцыя  ёсць  дыферэнцавальная ў пункце .  Пры гэтым

 .

□ На падставе дыферэнцавальнасці функцый g і f  маем

 .

Пры гэтым,  калі , то , таму што  ёсць непарыўная. Далей разгледзім

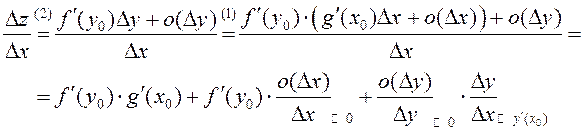
Калі  ў гэтай роўнасці перайсці да ліміту пры , атрымаем

 .   ■

Прыклад 1. Вылічыць вытворную функцыі .

► Гэтая функцыя ёсць кампазіцыя дзвюх  . Згодна з тэарэмаю маем  ◄

Прыклад 2. .

►  . ◄

Прыклад 3. .

►  . ◄

Тэарэма 2 (інварыянтавасць формы дыферэнцыяла).  Дыферэнцыял функцыі  мае адзін і той самы выгляд  не гледзячы на тое, ці ёсць x  незалежная зменная, ці х – дыферэнцавальная функцыя  якой-небудзь іншай зменнай.  

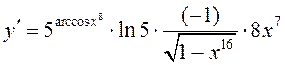□  Няхай  ёсць дыферэнцавальная функцыя зменнай t . Тады складаная функцыя  мае вытворную , а таму

. ■

Гэтую ўласцівасць дыферэнцыяла называюць інварыянтавасцю формы дыферэнцыяла.

Табліца асноўных вытворных:

§3.5. Вытворныя вышэйшых парадкаў.

def. Калі функцыя  мае вытворную ва ўсіх пунктах некаторай акругі пункта , а функцыя  ёсць дыферэнцавальная ў пункце , то вытворную ад апошняй функцыі называюць другою вытворнаю або вытворнаю другога парадку функцыі  у пункце  і абазначаюць .

Такім чынам .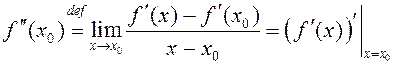

def. Няхай функцыя  мае ва ўсіх пунктах некаторай акругі пункта  вытворныя .Калі ў пункце  існуе вытворная функцыі , то яе называюць вытворнай n-га парадку функцыі  у пункце  і абазначаюць , г. зн.

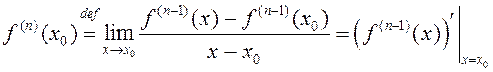                 (1)

def. Функцыю, якая мае на некаторым мностве Х вытворныя да n-га парадку ўлучна, называюць n разоў дыферэнцавальнаю на Х. Функцыю, якая мае на Х вытворную любога парадку, называюць бясконца дыферэнцавальнаю на Х. Напрыклад – бясконца дыферэнцавальная на .

Заўвага.Маецца пэўная зручнасць лічыць, што вытворная нулявога парадку супадае з самою функцыяй . Таму на падставе (1) атрымліваецца, што вытворная першага парадку ёсць вытворная функцыі.