Метадам матэматычнай індукцыі няцяжка атрымаць формулы для вылічэння вытворных вышэйшых парадкаў асноўных элементарных функцый.
1º. Ступеневая функцыя: ![]() .
.
![]() . Па
індукцыі
. Па
індукцыі ![]() .
.
У прыватнасці, калі ![]() , то
, то ![]() . Такім чынам, n-я вытворная мнагаскладу m-й ступені ёсць роўная нулю, калі n>m
. Такім чынам, n-я вытворная мнагаскладу m-й ступені ёсць роўная нулю, калі n>m ![]() . Чаму роўная
. Чаму роўная ![]() ?
?
![]()
2º. Паказнікавая функцыя: ![]() .
.
![]() . Па
індукцыі
. Па
індукцыі
![]() .
У прыватнасці
.
У прыватнасці ![]() .
.
3º. Лагарыфмічная функцыя: ![]()
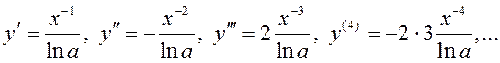 .
.
Па індукцыі 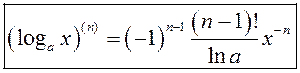 .
.
У прыватнасці ![]() .
.
4º. Сінус і косінус: ![]() .
.
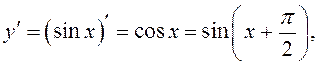
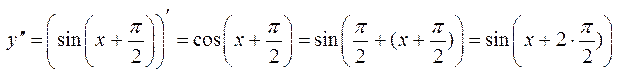 .
.
Па індукцыі 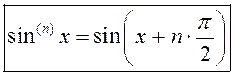 .
.
У прыватнасці ![]() ,
,
![]() .
.
Аналагічна 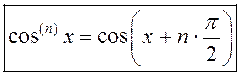 .
.
У прыватнасці ![]() ,
,
![]() .
.
На падставе атрыманых формул пры А=const., маем:
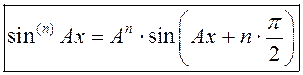 ,
, 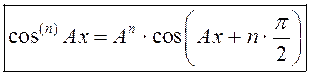 .
.
5º. Гіпербалічныя функцыі: ![]()
На падставе табліцы вытворных маем:
![]() .
.
У той час як правіла вылічэння першай
вытворнай ад сумы дзвюх функцый ![]() лёгка
пераносіцца на выпадак n-й вытворнай
лёгка
пераносіцца на выпадак n-й вытворнай ![]() ,
пры вылічэнні n-й вытворнай ад здабытку дзвюх функцый
узнікаюць пэўныя цяжкасці. Як вядома
,
пры вылічэнні n-й вытворнай ад здабытку дзвюх функцый
узнікаюць пэўныя цяжкасці. Як вядома ![]() . Але
. Але
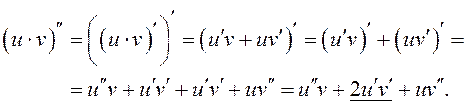
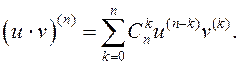
□ Доказ правядзем метадам матэматычнай індукцыі.
Няхай ![]() .
. 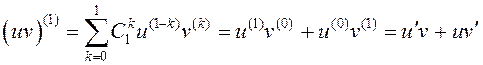 . Формула праўдзівая.
. Формула праўдзівая.
Дапусцім, што формула праўдзіцца для n=m.
Разгледзім
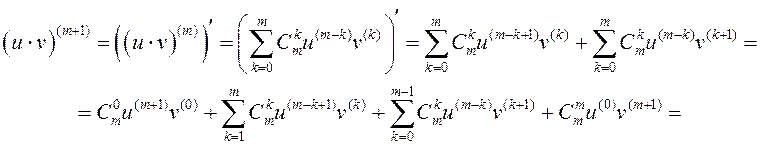
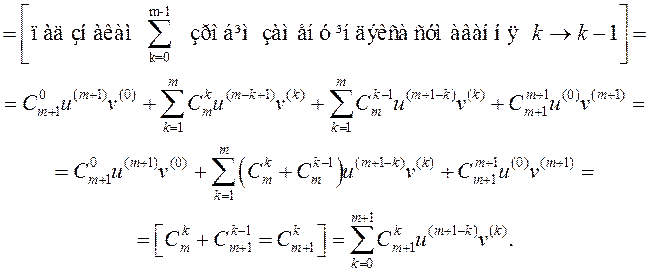
■
► Возьмем ![]() . Маем
. Маем
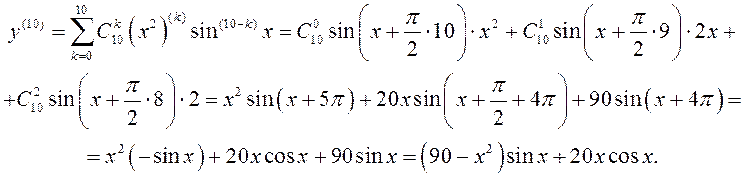
◄
► Возьмем ![]() . Маем
. Маем
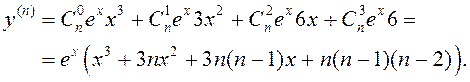
◄
def. Калі функцыя ![]() ёсць
дыферэнцавальная ў некаторай акрузе пункта
ёсць
дыферэнцавальная ў некаторай акрузе пункта ![]() ,
то яе дыферэнцыял
,
то яе дыферэнцыял
![]()
![]() =
= ![]() (1)
(1)
называюць першым дыферэнцыялам функцыі ![]() у
пункце
у
пункце ![]() .
.
Калі пры гэтым дыферэнцыял ![]() , які супадае з прыростам
, які супадае з прыростам ![]() незалежнай зменнай
незалежнай зменнай ![]() , не мяняецца, то
дыферэнцыял
, не мяняецца, то
дыферэнцыял ![]() ёсць функцыя толькі ад
ёсць функцыя толькі ад ![]() (
(![]() ).
).
def. Дыферэнцыял ад функцыі ![]() ў
пункце
ў
пункце ![]() называюцьдругім
дыферэнцыялам, або дыферэнцыялам другога парадку функцыі
называюцьдругім
дыферэнцыялам, або дыферэнцыялам другога парадку функцыі ![]() у пункце
у пункце ![]() і абазначаюць
і абазначаюць
![]() .
.
Выкарыстоўваючы формулу (1) і ўлічваючы, што ![]() , атрымоўваем
, атрымоўваем
![]() .
.
Па індукцыі вызначаецца
![]()
![]()
калі ![]() .
.
Пры гэтым няцяжка паказаць метадам матэматычнай індукцыі, што
![]() (2)
(2)
Адсюль атрымліваем
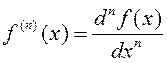
– яшчэ адзін спосаб для абазначэння вытворнай n – га парадку .
Калі разгледзець ідэнтычную функцыю ![]() то з формулы (2) вынікае,
што
то з формулы (2) вынікае,
што ![]()
![]()
![]() .
.
Заўвага. Дыферэнцыялы вышэйшых парадкаў, у адрозненні ад
першага дыферэнцыяла, не маюць уласцівасці інварыянтавасці формы, г. зн.
формула (2) не праўдзіцца, калі замяніць ![]() на
функцыю
на
функцыю ![]() .
.
Сапраўды, ![]() ёсць
складаная функцыя і таму
ёсць
складаная функцыя і таму ![]() Адкуль
атрымліваем
Адкуль
атрымліваем
![]() , або
, або
![]()
– у адрозненні ад фрмулы (2) тут маецца дадатковы складнік ![]() . Але, калі
. Але, калі ![]() , то
, то ![]() , і ў гэтым выпадку выгляд
другога дыферэнцыяла не змяняецца.
, і ў гэтым выпадку выгляд
другога дыферэнцыяла не змяняецца.
Па гэтай прычыне пры вылічэнні дыферэнцыялаў складаных функцый больш зручным уяўляецца выкарыстанне паслядоўнага вылічэння: спачатку вылічаецца першы дыферэнцыял, затым другі і г.д.
Пры вылічэнні дыферэнцыялаў выкарыстоўваюць наступныя правілы:
1. ![]()
![]() 4.
4.
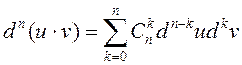
![]()
2. ![]() 5.
5.
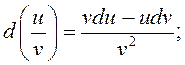
3. ![]()
![]()
![]() 6.
6.
![]() .
.
Прыклад: Вылічыць ![]() функцыі
функцыі ![]()
![]()
► 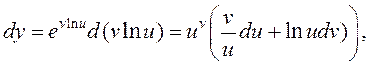
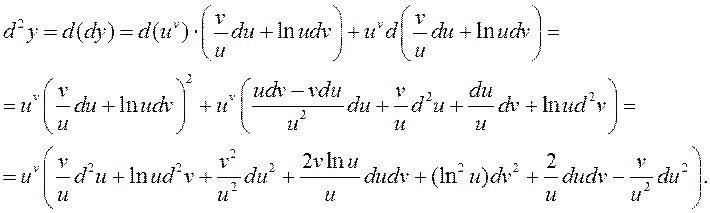
◄
1º. Параметрычная функцыя.
Няхай на некаторым прамежку Т лікавай восі t зададзены дзве функцыі
![]() ,
, ![]() (1)
(1)
Калі функцыя ![]() ёсць
строга манатонная, то існуе адваротная функцыя
ёсць
строга манатонная, то існуе адваротная функцыя ![]() ,
якая вызначана на мностве
,
якая вызначана на мностве ![]() .
Разгледзім складаную функцыю
.
Разгледзім складаную функцыю ![]() ,
вызначаную на мностве
,
вызначаную на мностве ![]() . Кажуць, што функцыя
зададзена параметрычна роўнасцямі (1).
. Кажуць, што функцыя
зададзена параметрычна роўнасцямі (1).
Калі ![]() і
і
![]()
![]() непарыўныя
на Т, то адваротная функццыя
непарыўныя
на Т, то адваротная функццыя ![]() ёсць
непарыў-ная на
ёсць
непарыў-ная на ![]() , а таму складаная
функцыя
, а таму складаная
функцыя ![]()
![]() таксама
непарыўная на
таксама
непарыўная на ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.