The skiving, which is a very efficient machining technology for processing short form surfaces of revolution, страница 3

In the chapter, a general interaction in the cutting system has been studied from the modern point of view. A deep analysis of deformation, contact and heattransfer processes as well as applicable material models has been described and criticized. Moreover an up-to-day methods and approaches to predictive cutting modeling have been summarized. Finite element method (FEM) has been especially underlined. The state-of-the-art FE analysis (FEA) software has been also outlined. According to given study a complete conclusion has been represented and FEM application to skiving modeling has been substantiated.

In the first section “A General Model of Interaction of Phenomena and Processes in Manufacturing System”, it has been brought into notice that the general cutting process carried out in manufacturing system is defined by rather complex tool-chip interaction with a great variety of randomness. The tool, chip and workpiece constitute a set named  working system. The possibility of the reduction of all known cutting processes to only “classical” orthogonal or oblique cutting scheme, which are convenient for analyses and modeling, based on their strong classification has been highlighted. Three well-known classification systems have been outlined.

In the second section “The Modern Models of Cutting Mechanics” a description of known chip formation models has been given. It involves an interaction among deformation, contact, heattransfer and material property modification processes. A modern comprehension of all mentioned processes has been outlined. It has been pointed out that there are three physical phenomena, which are primarily responsible for making metal cutting process and its numerical simulation very complex. The working cutting physical model has been assumed as in the figure 4.

The first is the large strain and high strain-rate plastic deformation in a concentrated shear region, i.e. primary deformation zone. It is well known that the shape of chips produced in metal cutting generally depends on the geometry of cutting tool, cutting conditions and tool-work materials used. There are three basic types of chip-forms, which can be identified: discontinuous chip, continuous chip and continuous chip with built-up edge. The amount of known analytical methods for prediction shear angle, shear stress, chip ratio, cutting forces under continuous chip formation have been generalized to common equations. In spite of rather long history of metal cutting theory it seems to have a great variety and usage limitation of the equations mentioned above. However, the Oxley shear angle and Kushner shear stress equation coefficients together with uniform shear stress distribution along shear plane for analytical modeling of structural steel skiving by carbide tool have been chosen as  preferable ones.

Another physical phenomenon is the contact and friction between the chip and cutting tool. The exact method by which friction works at the rake and flank faces is still a topic of great scientific interest but obey to general statements. However, this is not a usual friction process that most tribologists are familiar with because of high normal stress and juvenile contact surfaces on the tool-chip interface can be usually observed. The hypothesis of unvaried specific friction forces, which depend only on real ultimate tension, has been assumed. It has been also accepted that there are sticking (usually called secondary deformation zone) and sliding (Coulomb law) regions in the tool-chip interface. Moreover, the shear stress variation has been also assumed to be under mixer rule.

The third physical phenomenon is heattransfer process, which appears due to heat generation both in the irreversible plastic deformations and friction in chip-tool-workpiece interface. It has been noted that plastic and frictional work does not convert into the heat completely but rather small fraction of it usually converts into a change in the internal energy of cutting system. It is important that this fraction increases with deformation rate. It has been pointed out that heattransfer under cutting obeys the general heattransfer equation and therefore this equation can be applied to temperature field problem under cutting. The results obtained by Reznikov, Ostafiev, Silin etc. have been analyzed. It has been shown that the maximum of chip-tool contact temperature is usually appears in the middle of contact length and can achieve  a work material melting point. At the same time, the heat flow to the tool is minimum among those to the chip, workpiece and tool. It has been emphasized that there are two possible approaches for a heattransfer analysis under cutting: heat source approach and general FEM. As it has a great range of assumptions, the former was widely used about two decades ago. FEM becomes more and more popular because of its accuracy and flexibility.

It has been shown that work material model chosen influences   on result accuracy. For cutting modeling under continuous chip formation, elasto-plastic with linear hardening material model can be assumed and stress-strain relation has been excerpted from Von Misses as follows:

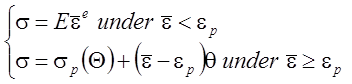,                                         (1)

where  - module of hardening;  - temperature;  - effective yield stress;  - yield strength;  - elastic strain;  - axial strain;  - ultimate plastic strain.

It has been emphasized that work material has to be the determined by following properties: Young module , Poisson’s ratio , yield strength , ultimate strength , real ultimate tensile , module of hardening , coefficient of linear expansion , density , thermal conductivity coefficient , specific heat . It has been pointed up that not only temperature dependency of the steel properties has been taken into account but also steel phase transition which usually takes place under heating to a high temperature.