Случайные события (Понятие случайного события. Вероятность случайного события. Основные теоремы и формулы. Повторение испытаний), страница 4

Пусть производится n одинаковых экспериментов, в каждом из которых может произойти одно из несовместных событий , образующих полную группу.

Все события рассматриваются на одном пространстве элементарных исходов W. Для моделирования последовательности испытаний построим новое пространство элементарных исходов :  ,

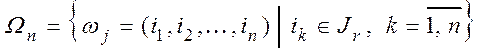где ;  – номер случайного события, произошедшего в k-м испытании;  – последовательность длины n номеров событий, произошедших в каждом из испытаний.

Пусть 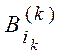 – случайное событие, которое заключается в том, что в k-м испытании произошло событие с номером , тогда

;

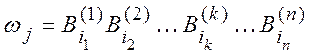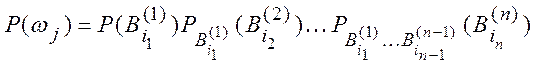
Последовательность испытаний называется независимой, если результаты предшествующих испытаний не влияют на результаты последующих испытаний.

В этом случае естественно считать, что условные вероятности перечисленных выше событий совпадают с безусловными вероятностями

.

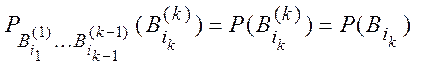Обозначим вероятности событий  через , т.е. , тогда

 ,                                              (1.10)

где .

Если  – обычная алгебра случайных событий, то

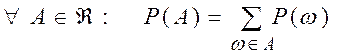                                       (1.11)

Получили вероятностное пространство, которое называется полиномиальной схемой.

Рассмотрим частный случай полиномиальной схемы – схему Бернулли.

1.4.1. Схема Бернулли

Рассмотрим два противоположных события, т.е. . В каждом испытании может произойти лишь одно случайное событие. Считаем, что испытания независимы, т.е. применима формула (1.10). Если в k-м испытании произошло событие А, то этот исход назовем успехом и припишем ему значение равное 1. Если в k-м испытании событие А не произошло, то это неудача, припишем этому исходу значение, равное 0. Тогда

,

где  – последовательность длины n, состоящая из 0 и 1.

Обозначим вероятность события , тогда .

Пусть  – число успехов в n испытаниях, тогда по формуле (1.10) вероятность произвольного исхода будет равна

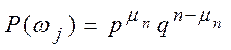.                                                (1.12)

Наибольший интерес в этой схеме представляет случайное событие , заключающееся в том, что в n независимых испытаниях событие А произошло m раз.

Теорема 1.1. Вероятность события  вычисляется по формуле

                                      (1.13)

– формула Бернулли.

Доказательство. В соответствии с определением вероятности случайного события (1.11), (1.12) получаем

,

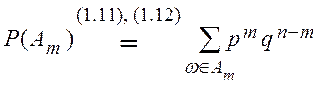где .

Необходимо найти только число элементарных исходов, благоприятствующих событию , а это число будет совпадать с числом способов, которыми в последовательности длины n можно выбрать m номеров испытаний, в которых произошло событие А, т.е. , откуда и следует формула (1.13).  

Пример 1.11. Что вероятнее выиграть у равносильного шахматиста: две партии из четырех или три из шести (ничьи не учитываются).

Решение. Событие А – выигрыш в партии одним из игроков, тогда по условию

.

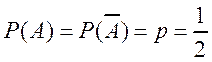1)  При n = 4, m = 2 по формуле (1.13) находим

;

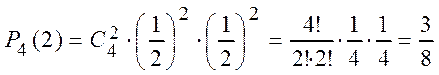2)  При n = 6, m = 3, получаем

,

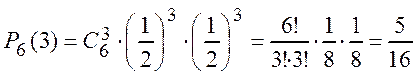т.е. вероятность выигрыша двух партий из четырех больше, чем трех из шести.

1.4.2. Общая полиномиальная схема

Рассмотрим общую полиномиальную схему сr случайными событиями и найдем вероятность случайного события , которое заключается в том, что событие  произошло  раз, событие  произошло  раз, …, событие  произошло  раз .

Теорема 1.2. Вероятность события  вычисляется по формуле

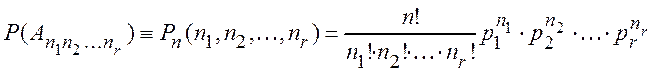         (1.14)

где .

Доказательство. Вероятность этого случайного события

.

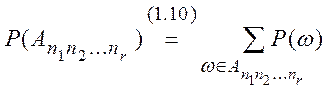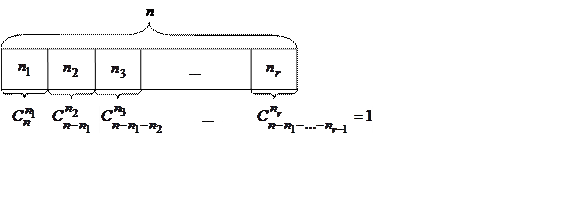Осталось найти число элементарных исходов, благоприятствующих событию . Это число будет равно числу способов, которыми в последовательности длины n можно выбрать  номеров испытаний, в которых произошло событие ,  номеров испытаний, в которых произошло событие , …,  номеров испытаний, в которых произошло событие  (см. схему), т.е. общее число способов будет равно

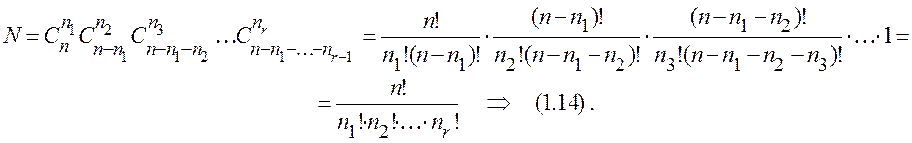
            Здесь в каждой паре соседних дробей в числителе и знаменателе есть общие множители, поэтому большая часть сомножителей сокращаются.

Пример 1.12. Какова вероятность выиграть три партии из шести, две свести вничью и одну проиграть у равносильного шахматиста.

Решение. Пусть  – выигрыш партии одним из игроков,  – партия завершилась вничью,  – проигрыш партии одним из игроков. Теперь

,  ,  .

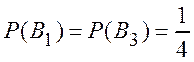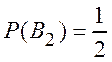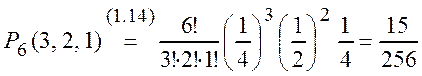1.4.3. Наивероятнейшее число появлений события в схеме Бернулли

По формуле Бернулли,   , где  , найдем отношение

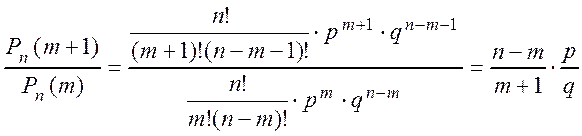.  Если 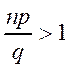, то

 ;   .

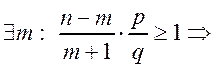
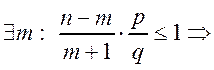
Значит существует  – наивероятнейшее число появлений события А. Рассмотрим второе неравенство

,  .

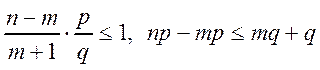1)  Если  – целое число, то пусть  и тогда

,

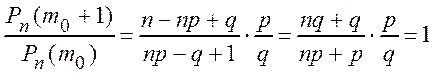таким образом , т.е.  два наивероятнейших числа появлений событияА в испытаниях.

2)  Если  – нецелое число, то обозначим через  – наименьшее целое число большее , т.е. в этом случае  определяется как решение неравенств

   или   .

1.4.4. Предельные теоремы в схеме Бернулли

По формуле Бернулли (1.14), в том случае когда число испытаний очень большое, а вероятность появления или непоявления события А мала, ничего посчитать практически невозможно. В этом случае перемножаются очень большие числа и очень маленькие и за счет ошибок округления возникают большие погрешности. В данной ситуации используются приближенные формулы.

Теорема 1.3. (Пуассона)

Если при  так, что , тогда

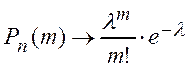                                                                                                             (1.15)

Доказательство. Обозначим 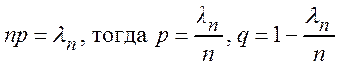, и по формуле Бернулли

.

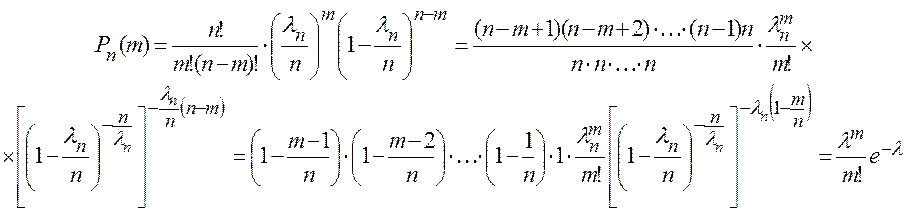
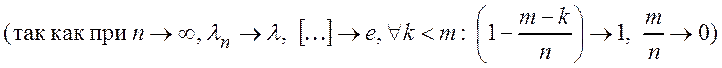 справедлива приближенная формула Пуассона

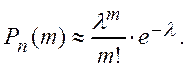
Пример 1.13. Пекарня выпекает булочки с изюмом, среднее число изюминок в булочке равно 5. Что вероятнее: купить булочку с 4 или с 6 изюминками.

Решение. По формуле Пуассона (1.15) находим

,  ,   .

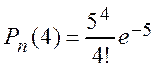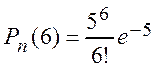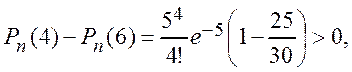
Теорема 1.4 (локальная теорема Лапласа)

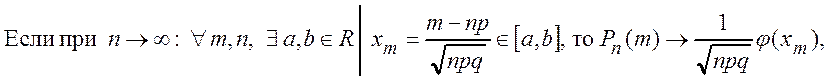
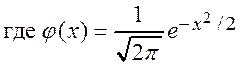 – локальная функция Лапласа.

Доказательство. Из условия 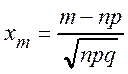 находим

                      (*),

          (**).

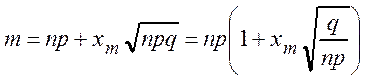
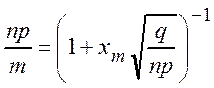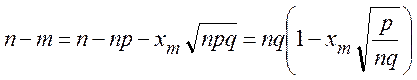
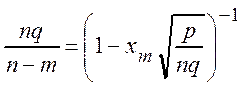Из (*), (**) .

Далее используем формулу Стирлинга   ,  где 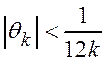, таким образом

, , .

Подставляя в формулу Бернулли, получаем

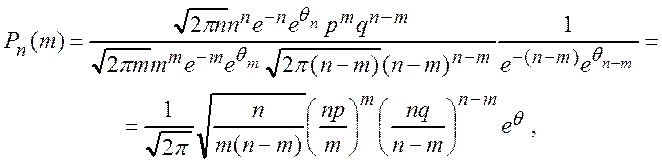
где , причем .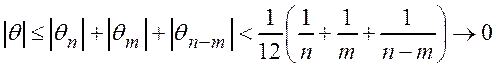

Обозначим 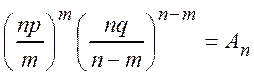 и вычислим логарифм .

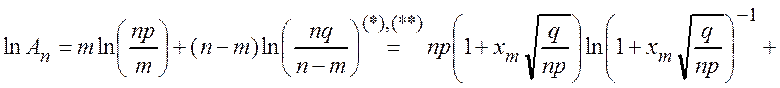
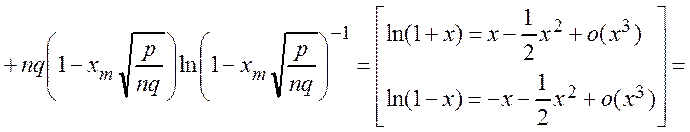
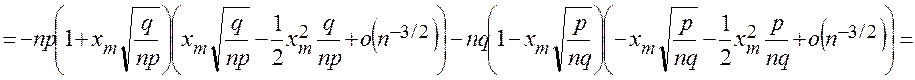
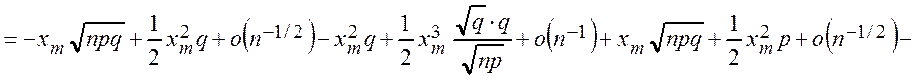
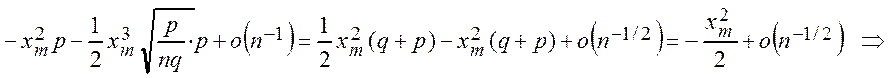
Þ .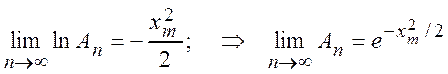

            Рассмотрим первый множитель

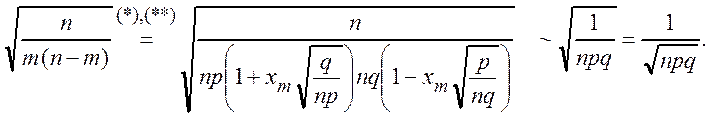
Таким образом

.

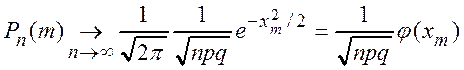При  , справедлива локальная формула Муавра-Лапласа

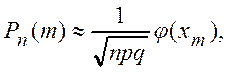                                           (1.16)

где.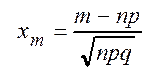

Теорема 1.5 (интегральная теорема Лапласа)

При   :   ,

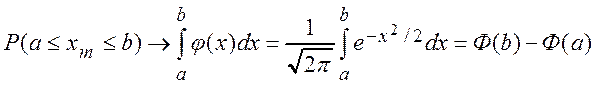где 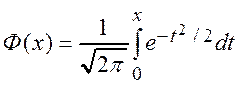  – интегральная функция Лапласа.

Доказательство.  ,

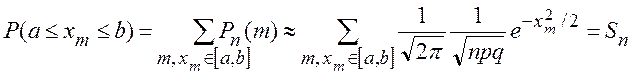здесь 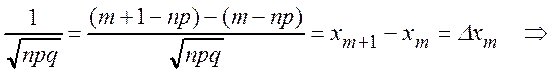  S_n – интегральная сумма для функции 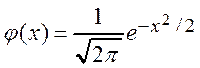. Переходя к пределу при , получим нужный результат.

Если , то справедлива интегральная формула Лапласа

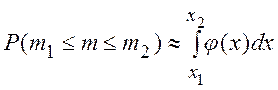                                                      ,                                        (1.17)

где .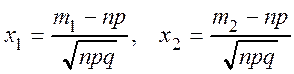

Пример 1.14. Вероятность появления события А в одном испытании равна          p = 0,7. Найти вероятность того, что в 100 независимых испытаниях событие А произойдет от 60 до 90раз.

Решение. Решим поставленную задачу приближенным способом с помощью интегральной теоремы Лапласа:

,

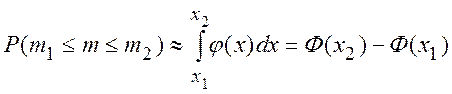где .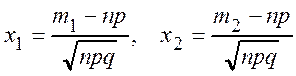

Находим:

.

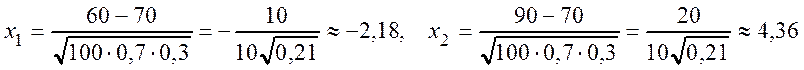Таблица значений интегральной функции Лапласа Ф(x) для положительных x приведена в приложении 2. Причем функция Ф(x) – нечетная, т.е. .

Для всех значений x > 4 принимают . В нашем случае:

.