Случайные события (Понятие случайного события. Вероятность случайного события. Основные теоремы и формулы. Повторение испытаний), страница 2

Числовая функция, заданная на алгебре случайных событий, называется вероятностью, если выполняются следующие аксиомы:

А1 (аксиома неотрицательности):  .

А2 (аксиома нормированности): .

А3 (аксиома аддитивности):  для любых двух несовместных событий

.

Следствие 1.1.

,

.                                                       (1.1')

Доказательство.  .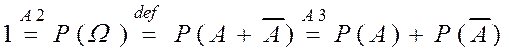

Следствие 1.2.

.

Доказательство. Так как , используя равенство (1.1'), получаем

.

Следствие 1.3.  .

Доказательство. , так как

.

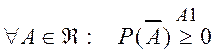Следствие 1.4 (теорема сложения).

.                                       (1.2)

Доказательство. Покажем, что

,                                                          (*)

действительно,  .

С другой стороны

,                                                            (**)

действительно

.

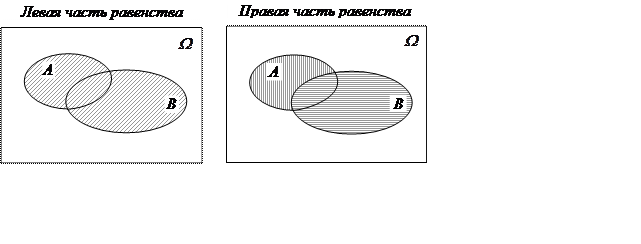В правых частях равенств (*) и (**) суммы несовместных событий:

 – несовместны,

 – несовместны.

Таким образом,

, .

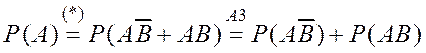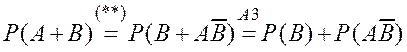Вычитая из второго равенства первое, получаем

,  .

Для трех слагаемых, аналогично

  (1.3)

Доказательство. Пусть  тогда

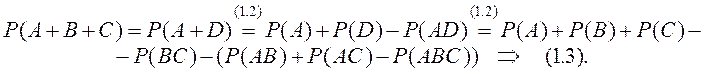
            Для большего числа случайных событий вероятность суммы вычисляется по формуле (как выяснится позже, вероятность совместного появления большого числа событий найти проще, чем вероятность суммы):

.

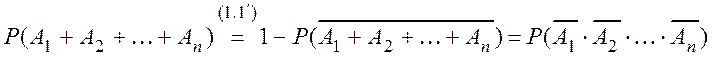1.2.2. Конечная вероятностная схема

Тройка  называется вероятностным пространством.

Пусть в этом вероятностном пространстве пространство элементарных исходов  – конечное множество.

Припишем каждому элементарному исходу некоторое неотрицательное число , для которых выполняются два свойства:

;  ;

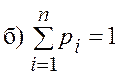тогда  определим функцию Р с помощью равенства

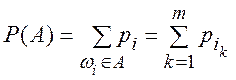  ,                                                  (1.4)

где  – номера элементарных исходов, которые благоприятствуют событию А, т.е. ;   – вероятности элементарных исходов.

Формула (1.4) – определение вероятности в конечной схеме.

Таким образом, вероятность случайного события– это сумма вероятностей элементарных исходов, благоприятствующих данному событию.

Классическое определение вероятности.

Если в некотором смысле вероятности элементарных исходов одинаковы, т.е. элементарные исходы равновозможные, то логично считать, что

,

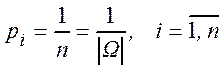в этом случае условия а) и б) выполняются:

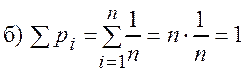,  , тогда

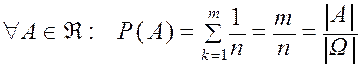.                                     (1.5)

Вероятность случайного события равна отношению числа элементарных исходов, благоприятствующих событию А, к общему числу равновозможных элементарных исходов.

В примере 1.2 (с игральными костями) , тогда

.

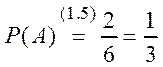Пространство элементарных исходов в каждом случае выбирается наиболее подходящим образом. Довольно часто этот выбор не всегда очевиден. Рассмотрим простой пример.

Эксперимент – подбрасывание двух одинаковых монет, событие А – монеты выпали одинаковыми сторонами. Рассмотрим два варианта решения.

Модель 1.1. , где  – монеты выпали "гербами",  – монеты выпали "решками",  – монеты выпали разными сторонами, тогда ,

.

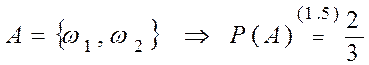Модель 1.2. , где  – монеты выпали "гербами",  – выпали "герб" и "решка",  – выпали "решка" и "герб",  – монеты выпали "решками", тогда ,

   .

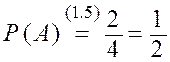            Какое из этих решений более соответствует истине сразу, вообще говоря, не понятно. В первом случае монеты не различимы, во втором случае они считаются разными. В этих случаях помогает статистическое определение вероятности (критерий истины – это практика). Но прежде еще один пример.

Парадокс де Мере. Многократно наблюдая игру в кости, шевалье де Мере обратил внимание, что при подбрасывании трех игральных костей сумма очков, равная 11, появляется чаще, чем сумма очков, равная 12, хотя число элементарных исходов, благоприятствующих тому и другому событию, одно и то же. 

å = 11:  6–4–1,  5–4–2,  4–4–3,  5–5–1,  6–3–2,  5–3–3;

å = 12:  6–5–1,  5–5–2,  4–5–3,  4–6–2,  4–4–4,  6–3–3.

            В чем здесь дело?

1.2.3. Статистическое определение вероятности

Рассмотрим последовательность из N экспериментов, в каждом из которых может произойти некоторое событие А.

Обозначим через  число испытаний, в которых событие А произошло, тогда 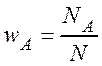– относительная частота появления события А в этих испытаниях.

Если при увеличении N относительная частота незначительно отклоняется от некоторого числа р, то это число называется вероятностью события А, т.е. в соответствии со статистическим определением вероятности

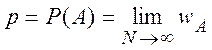
1.2.4. Геометрическая вероятность

Идея: представить пространство элементарных исходов в виде некоторого множества пространства , тогда любое случайное событие – это подмножество данного множества и

,

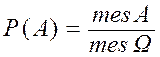где mesC – мера множества , т.е. приn = 1  mesC – длина промежутка, при        n = 2 mesC – площадь плоской фигуры, при n = 3  mesC – объем тела.

Задача о встрече. Два лица договорились встретиться в определенном месте от 12.00 часов до 13.00 часов с условием, что пришедший первый ждет другого 20 минут и, если не дожидается, то уходит. Какова вероятность встречи?

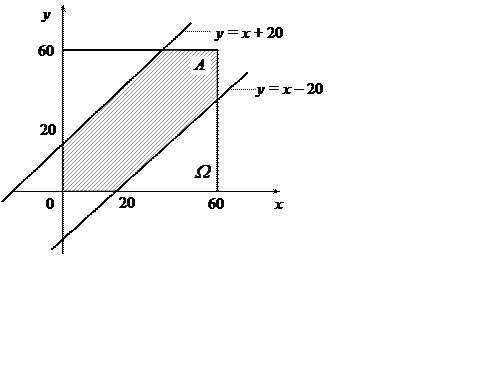Решение. Событие А – встреча состоялась. Пусть x – время прихода к месту встречи одного, y – время прихода к месту встречи другого. Возможные элементарные исходы это точки квадрата со стороной        60 мин, т.е. . Тогда событие А – это подмножество из :

.

,

строим множество А по граничным линиям:

  ;    

 – отношение площадей фигур А и , тогда

.

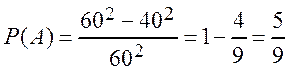1.3. Основные теоремы и формулы

1.3.1. Условная вероятность и теорема умножения

Рассмотрим произвольное вероятностное пространство  и два события А и В. Будем считать, что .

Что можно сказать о вероятности события В, если известно, что произошло событие А?

Тот факт, что событие А произошло, несет некоторую дополнительную информацию о пространстве элементарных исходов, что, возможно, изменяет вероятность появления В.

По определению вероятность события В, найденная в предположении, что произошло некоторое событие А, называется условной вероятностью события В (обозначается ).

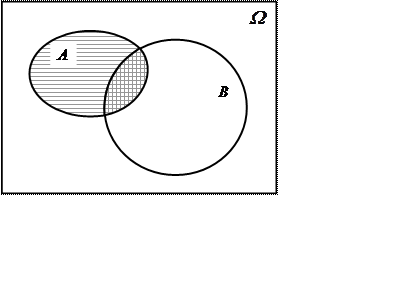Если событие А произошло, то некоторые из элементарных исходов становятся невозможными, , и мы можем рассматривать новое усеченное пространство элементарных исходов, из которых невозможные исходы исключены, т.е. .

Например, при классическом определении вероятности условную вероятность можно подсчитать в этом новом пространстве элементарных исходов следующим образом:

, .

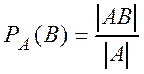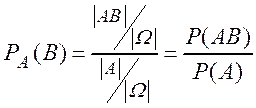Условной вероятностью события В называется число, равное отношению вероятности совместного появления событий к вероятности события А.

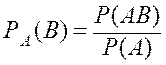 .                                                   (1.6)

Условная вероятность, определенная таким образом, удовлетворяет всем аксиомам А1 – А3 в определении вероятности.

Действительно:

1)  так как 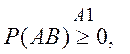   ( по условию), то

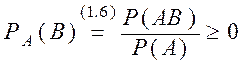  Þ  А1 справедлива;

2) 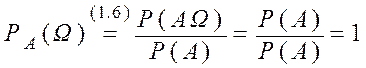   Þ  А2 справедлива;

3)  Если В и С несовместные события, т.е. , то события АВ и АС тоже несовместны , тогда

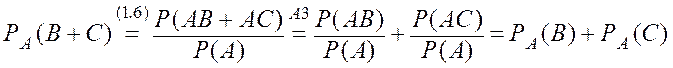 Þ А3 справедлива.

Пример 1.6. Студент идет на экзамен, зная первые пять билетов из первого десятка и пять последних билетов из третьего десятка. Общее количество билетов 30. Ему достается билет из первого десятка. Найти вероятность того, что билет знаком студенту.