Решение. Пусть событие А – билет извлечен из первого десятка, событие В – билет знаком студенту. Тогда
![]() ,
, ![]() ,
, 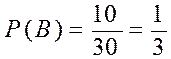 .
.
![]() ,
, ![]()
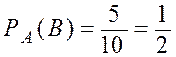 .
.
Если использовать формулу (1.6), то
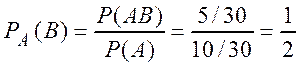 .
.
Равенство (1.6) можно представить в следующем виде
![]() (1.7)
(1.7)
– теорема умножения, или
![]()
Эти формулы легко обобщаются на случай nсомножителей
![]() (1.8)
(1.8)
Доказательство этой формулы проводится по индукции. При n = 2 равенство (1.8) справедливо (см. формулу (1.7)). Предположим, что оно справедливо для n – 1 сомножителей , тогда обозначим
![]()
и запишем формулу (1.7).
![]() ,
,
откуда
следует справедливость формулы (1.8) ![]()
Пример 1.7. Студент идет на экзамен, выучив 15 из 30 вопросов. Ему предлагают билет из трех вопросов. Найти вероятность того, что студент знает все три вопроса.
Решение. Пусть
![]() , где
, где
![]() – i-й вопрос знаком студенту, тогда
– i-й вопрос знаком студенту, тогда
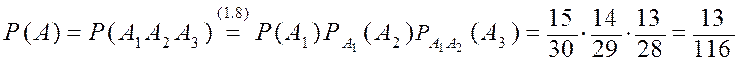 .
.
Событие В – хотя бы один вопрос знаком студенту, тогда
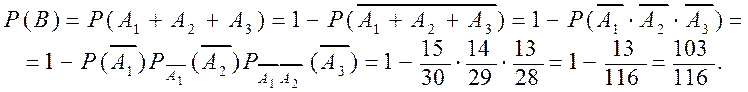
В общем случае имеем
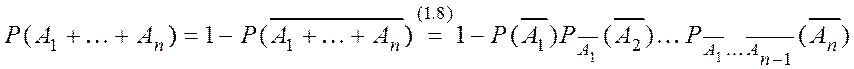
Если вероятность появления одного из событий не зависит от того, произошло ли другое, то эти события называются независимыми.
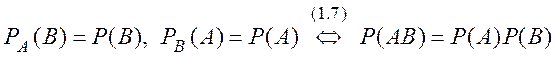 .
.
События ![]() называются независимыми в совокупности, если для любого
набора индексов
называются независимыми в совокупности, если для любого
набора индексов ![]() справедливы равенства
справедливы равенства
![]() или
или 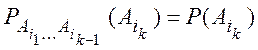 .
.
Из независимости в совокупности следует попарная независимость, но, вообще говоря, не наоборот, т.е. попарная независимость не является достаточным условием независимости в совокупности.
Пример 1.8. Пусть имеется урна с 4 шарами, в которой: 1 – белый шар, 1 – черный, 1 – красный, 1 – раскрашен в три цвета.
Решение. Событие А – извлеченный наудачу шар содержит в окраске белый цвет, событие В – извлеченный наудачу шар содержит в окраске черный цвет, событие С – извлеченный наудачу шар содержит в окраске красный цвет. Тогда
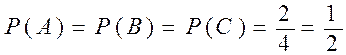 ,
, 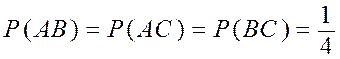 ,
,
и 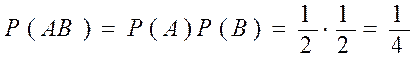 ,
,  ,
,
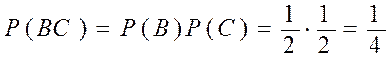 , т.е. события попарно независимы, но
, т.е. события попарно независимы, но 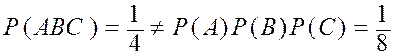 , или, например,
, или, например, 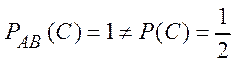 , следовательно события
, следовательно события ![]() зависимы в совокупности.
зависимы в совокупности.
1.3.2. Формула полной вероятности
События ![]() называются полной группой, если справедливо равенство
называются полной группой, если справедливо равенство ![]() , т.е. в результате эксперимента происходит хотя бы одно из этих
событий. Будем рассматривать полную группу попарно несовместных случайных событий,
т.е. таких, что
, т.е. в результате эксперимента происходит хотя бы одно из этих
событий. Будем рассматривать полную группу попарно несовместных случайных событий,
т.е. таких, что ![]() .
.
Для полной группы несовместных событий: ![]() .
.
Задача. Пусть некоторое событие А может произойти лишь при условии появления одного из событий, образующих полную группу. Причем заранее не известно, какое из этих событий произойдет (эти события называются гипотезами). Требуется найти вероятность события А.
Так как по определению ![]() , то событие А можно представить в виде
, то событие А можно представить в виде
![]() .
.
Причем в правой
части равенства записана сумма несовместных событий, так как ![]()
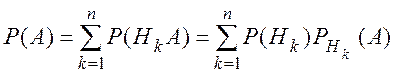 , т.е.
, т.е.
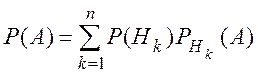 (1.9)
(1.9)
– формула полной вероятности
Пример 1.9. Студент идет на экзамен, зная 20 билетов из 25. Каким лучше зайти в аудиторию: первым, вторым или третьим? Одним словом, когда вероятность взять выученный билет больше?
Решение. Пусть событие А – студент взял знакомый билет.
Если студент заходит первым, то
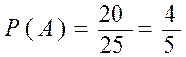 .
.
Если студент заходит вторым, то
относительно первого студента можно выдвинуть две гипотезы: ![]() – взял знакомый билет,
– взял знакомый билет, ![]() – взял незнакомый билет. В этом случае по формуле полной
вероятности находим:
– взял незнакомый билет. В этом случае по формуле полной
вероятности находим:
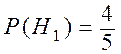 ,
, 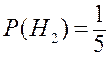 ,
, 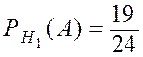 ;
; 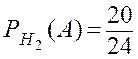 , и
, и 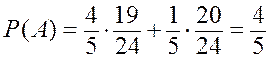 .
.
Если студент заходит третьим, то
относительно первых двух студентов можно предположить: ![]() – взяли два знакомых студенту билета,
– взяли два знакомых студенту билета, ![]() – взяли один знакомый, один незнакомый билет,
– взяли один знакомый, один незнакомый билет, ![]() – взяли два незнакомых билета, тогда
– взяли два незнакомых билета, тогда
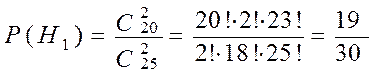 ,
, 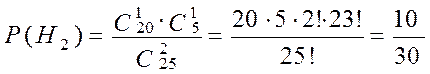 ,
,
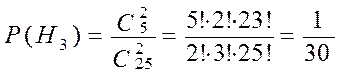 ,
, 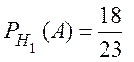 ,
, 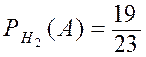 ,
, 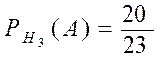 ,
,
тогда по формуле полной вероятности:
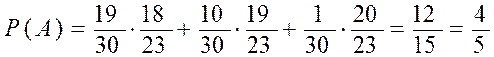 .
.
Видно, что во всех трех случаях вероятность получить выученный билет одна и та же, т.е. здесь "фортуну" обмануть нельзя.
1.3.3. Формулы Байеса
Предположим, что при выполнении условий предыдущей задачи (см. формулу (1.9)) в результате эксперимента событие А произошло. Этот факт несет дополнительную информацию об эксперименте, что приводит к тому, что первоначальные вероятности гипотез каким-то образом изменяются. Используя формулу (1.7), можно записать
![]()
Þ 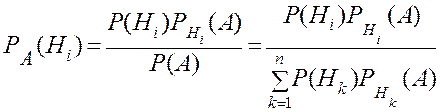
– формулы Байеса.
Здесь ![]() – априорные вероятности,
– априорные вероятности, ![]() –
апостериорные вероятности.
–
апостериорные вероятности.
Пример 1.10. Студент идет на экзамен, зная 20 билетов из 25, заходит вторым и берет знакомый ему билет. Какова вероятность того, что зашедший первым тоже взял знакомый ему билет? (см. предыдущий пример).
Решение.
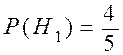 ,
, 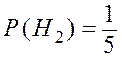 ,
, 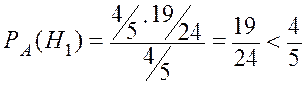 ,
, 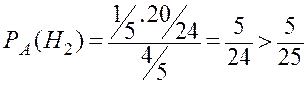 ,
,
так
как ![]() по-прежнему
образуют полную группу, то
по-прежнему
образуют полную группу, то
![]() .
.
1.3.4. Примеры решения задач
Задача о разорении игрока. Два игрока продолжают некоторую игру до полного разорения. Первый игрок имеет капитал в n1 рублей, второй – в n2 рублей. Вероятность того, что очередную партию выиграет первый, равна р, а вероятность того, что ее выиграет второй, равна q. Будем считать, что p + q = 1 (т.е. ничьих не бывает). Требуется найти вероятности разорения игроков.
Решение. Обозначим
через ![]() вероятность
того, что первый игрок, имея n рублей, разорился,
вероятность
того, что первый игрок, имея n рублей, разорился, ![]() –
второй игрок, имея n рублей, разорился. Тогда искомые вероятности есть
–
второй игрок, имея n рублей, разорился. Тогда искомые вероятности есть ![]() и
и ![]() .
.
Очевидно, выполняются соотношения (краевые условия):
![]() .
.
Так как в первом случае первый игрок собрал весь капитал, его разорение невозможно. Во втором случае у него не осталось ни рубля (он разорился). Перед очередной партией разорение первого игрока может произойти двумя способами:
а) ![]() – он выиграл очередную партию и
– он выиграл очередную партию и ![]() –
проиграл всю игру,
–
проиграл всю игру,
б) ![]() – он проиграл очередную партию и затем
– он проиграл очередную партию и затем ![]() – проиграл
всю игру. Здесь применима формула полной вероятности (стоимость выигрыша и
проигрыша 1 рубль).
– проиграл
всю игру. Здесь применима формула полной вероятности (стоимость выигрыша и
проигрыша 1 рубль).
![]() ,
, ![]() ,
,
![]() . (*)
. (*)
1)
Пусть ![]() ,
тогда из равенства (*), получаем
,
тогда из равенства (*), получаем
![]() ,
, ![]() ,
,
так
как ![]() ,
тогда из равенства
,
тогда из равенства ![]() Þ
Þ
![]() ,
, 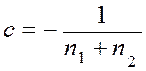 , т.е.
, т.е.
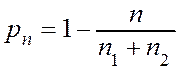 Þ
Þ 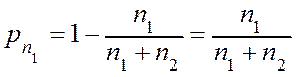 .
.
Аналогично 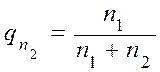 .
.
2) В общем случае, если p ¹ q из равенства (*) Þ
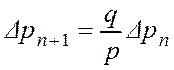 Þ
Þ 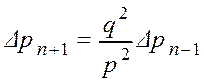 , … ,
, … , 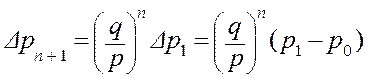 .
.
Так
как 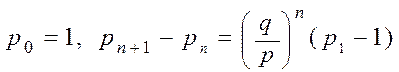 ,
, 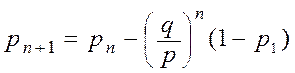 :
:
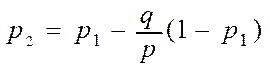 ,
, 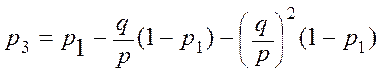 , … ,
, … ,
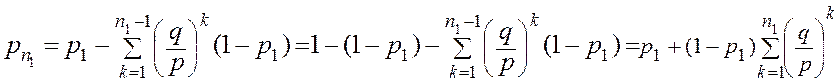 (**)
(**)
Из второго краевого условия находим:
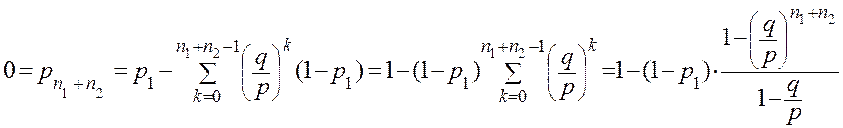 ,
,
откуда
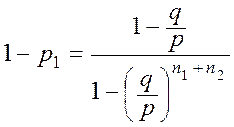 , из
равенства (**) Þ
, из
равенства (**) Þ
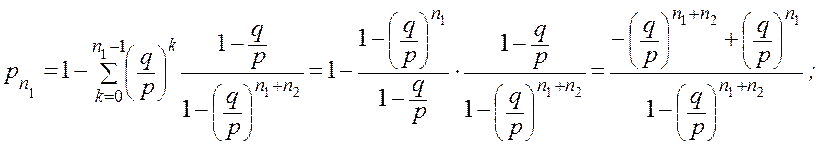
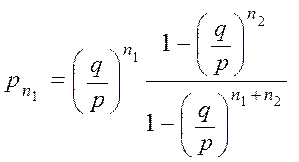 – вероятность разорения первого игрока,
– вероятность разорения первого игрока,
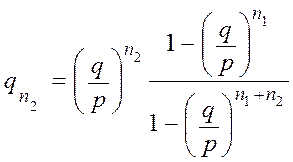 – вероятность разорения второго игрока.
– вероятность разорения второго игрока.
Пусть, например, капитал второго игрока ![]() . В
этом случае разорить второго игрока практически невозможно
. В
этом случае разорить второго игрока практически невозможно
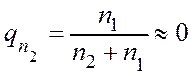 .
.
Если p >> q, то 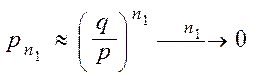 , так
как
, так
как 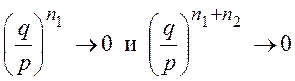 .
.
Задача о безотказной работе станка. Найти вероятность того, что станок, работавший в момент времени t0, не остановится в течение промежутка времени t0 + t при условиях:
1) вероятность остановки станка не зависит от величины промежутка (t0, t0 + t), т.е. от t,
2) вероятность остановки станка за малый промежуток времени Dt пропорциональна этому промежутку с точностью до бесконечно малой более высокого порядка.
Решение. Обозначим используемую вероятность через P(t), тогда из 2-го условия можно получить
![]()
–
за время Dt станок
остановится, где 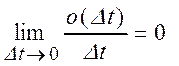 .
.
Вероятность бесперебойной работы станка за промежуток ![]() будет
равна вероятности совместного появления двух событий, т.е.
будет
равна вероятности совместного появления двух событий, т.е. ![]() (так
как по 1-му условию они независимы)
(так
как по 1-му условию они независимы)
![]()
![]() ,
,
разделим
на Dt и перейдем
к пределу при ![]() . Таким образом, слева получим определение производной и приходим к
дифференциальному уравнению с разделяющимися переменными
. Таким образом, слева получим определение производной и приходим к
дифференциальному уравнению с разделяющимися переменными
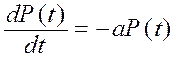 ,
, 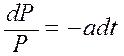 ,
, ![]() .
.
![]()
1.4. Повторение испытаний
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.