Оценка возможности транспортировки специальных изделий воздушным транспортом. Транспортировка системы “носитель-трал” военно-транспортной авиацией, страница 6

Первое из этих уравнений определяет форму, а второе характеризует распределение скоростей точек троса в начальный момент времени t=0.

Граничные условия:

U(0, t)= 0;

U(l, t)= 0 (8).

показывают, что перемещение точек закрепления троса равны нулю в любой момент времени.

2.5.1.  Решение волнового уравнения методом Фурье.

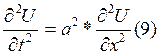 - исходное уравнение собственных колебаний троса.

Рассмотрим свободные колебания.

Будем искать решение уравнения (9) в виде:

U(t, x)= T(X)*X(x) (10).

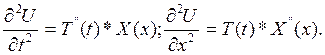
Следовательно, в уравнение (9):

T^”(t)*X(x)= a²*T(t)*X^”(x).

Дальше делим переменные:

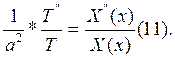
Утверждение: поскольку левая часть может зависеть только от t, а правая от x, то ни левая, ни правая части не зависят ни от t, ни от x и являются постоянными.

Почему: пусть левая часть зависит от t. Зафиксируем правую часть (x). Тогда в правой части при фиксировании (x), если менять t, то правая часть (константа) равняется нескольким числам слева, а это не может быть. Аналогичные утверждения можно провести с x.

Из равенства (11):

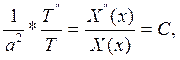
где С= const.

Последнее соотношение показывает, что функции X(x) и T(t) удовлетворяют следующим дифференциальным уравнениям:

T^”-c*a²*T= 0;

X^”-c*X= 0.

Рассмотрим X^”-c*X= 0 (12).

Из граничных условий (8) следует:

X(0)*T(t)= 0,

X(l)*T(t)= 0.

Так как T(t)0 хотя бы в одной точке (нас интересует тривиальное решение), то

X(0)= 0, X(l)= 0 (13).

Найдем решение уравнения (13).

1.Пусть С= 0, следовательно X^”= 0,

μ²= 0 – характеристическое уравнение, μ_1,2= 0.

X= C₁*e^μ₁^*x+C₂*x*e^μ₂^*x= C₁+C₂*x.

Определим С₁ и С₂:

X(0)=C₁+C₂*0= 0

X(l)= C₁*C₂*l

cледовательно,

C₁=0, C₂= 0, т. е. X(x)= 0.

2. Пусть c= λ², следовательно, X^”- λ²*X= 0.

μ²-λ²= 0

μ_1,2= λ

X(x)= C₁*e^λ*x+C₂*e^-λ*x

C₁+C₂= X(0)= 0

C₁*e^λ*e+C₂*e^-λ*e= 0

C₁= C₂= 0

X(x)= 0.

3. C=-λ²

X^”+ λ²*X= 0

μ²+ λ²= 0

μ_1,2=i*λ.

Т. е. Характеристическое уравнение имеет комплексно сопряженные корни μ₁ и μ₂.

Указанным корням соответствуют действительные решения дифференциального уравнения e^μ₁  и e^μ₂.

Из этих решений линейно-независимым является только e^μ₁^*x. В противном случае определитель Вронского равен нулю, т. е. получим нулевое решение.

X(x)= e^μ₁^*x *cosλ*x+C₂*sinλ*x

X(0)= C₁*1+C₂*0= 0

X(l)= C₁*cosλ*l+C₂*sinλ*l= 0

C₁= 0

C₂*sinλ*l= 0

Нас интересует случай, когда C₂ 0 (нетривиальное решение).

Получаем:

sinλ*l= 0, λ*l= π*k

λ= λ*k=  π*k/l ; k= 0,

Каждому  в λ_k соответствует:

X_k(x)= A_k*sinλ_kx= A_k*sin(k*π*x/l).

Число λ_k= k*π/l называются собственными числами, задачи (12), (13), а функции X_k(x)= A_k*sinλ_kx – собственными функциями.

Найдем T(t):

T^”(t)-c*a²*T= 0 при c= -λ²*k

T^”_k+λ²_k*a²*T= 0

μ²+ λ²_k*a²= 0

μ_1,2=i*λ_k*a

T_k(t)= B_k*cosλ_k*a*t+D_k*sinλ_k*a*t= B_k*cos(k*π*a*t/l)+D_k* sin(k*π*a*t/l)

Заметим, что k= 1, 2, 3. При k0 функции X_k(x) будут отличаться от соответственных функций для k>0 только значком, и можно включить в константу.

Т. е. каждому k соответствует функция:

U_k(t, x)= T(t)*X(x)

U_k(t, x)= [a_k*cos(k*π*a*t/l)+b_k* sin(k*π*a*t/l)]*sin(k*π*x/l) (14).

a_k= B_k*A_k

b_k= D_k*A_k

Функция (14) называется собственными функциями задачи о свободных колебаниях троса.

Определим  a_k и b_k.

Составим ряд:

U(t, x)=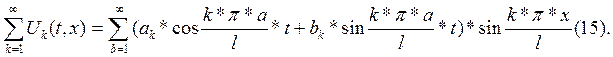

 

Будем предполагать, что этот ряд сходится, его можно почленно дифференцировать.

Подберем числа a_k и b_k так, чтобы выполнялись начальные условия (7).

Заметим, что функция U(t, x), определяемая равенством (15) удовлетворяет граничным условиям (8).

Мы получили решение (14) и используем (8) при определении значений констант C₁ и C₂.

Кроме того, эта функция является решением дифференциального уравнения (9).

Из равенства (15) при t= 0 получаем:

U(t= 0)=

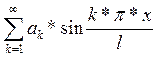
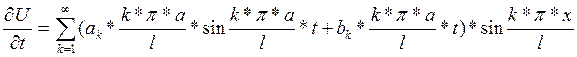
При t= 0 U^’_t= F(x)

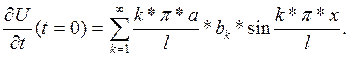
Для того, чтобы выполнялись начальные условия (7) необходимо:

U(t= 0)=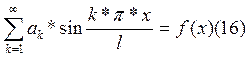

U^’(t= 0)=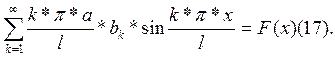

Для того, чтобы выполнялись (16) и (17) разложим f(x) и F(x) в ряд Фурье на промежутке [0, l] по sin.

Отступление: ряд Фурье по [-l, l].

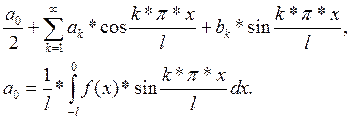
Ряд Фурье для нечетных функций (по sin) имеет вид:

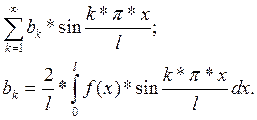
Равенство (16) будет разложением функции f(x) по sin, если:

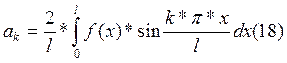
Равенство (17) будет разложением функции F(x) по sin, если:

 

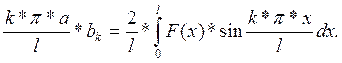
Следовательно, получаем:

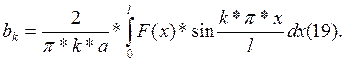
Т. е. функция U(t, x), удовлетворяющая уравнению (9), начальным условиям (7) и условию (8), определяется следующим образом: